
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Расчет осадки основания. Общие положения
Расчет осадки основания. Общие положения
| Проектирование основания следует выполнять на основе существующих нормативных документов в частности СНиП 2.02.01-83* "Основания зданий и сооружений" или СП 50-101-2004 "Проектирование и устройство оснований и фундаментов зданий и сооружений". Ниже мы рассмотрим, на основании каких положений можно определить осадку основания. |
Для начала выясним, что подразумевается под термином - осадка основания (обозначается литерой "s").
Осадка - это деформация, происходящая в результате уплотнения грунтов, залегающих ниже фундамента, под воздействием нагрузки от здания или сооружения, иногда под воздействием собственного веса вышележащего грунта.
При этом существенного изменения структуры грунтов не происходит и потому такую деформацию можно условно считать упругой. Это означает, что давление на основание (нагрузка от фундамента) должно быть меньше расчетного сопротивления грунта.
Если давление на грунт будет больше расчетного сопротивления грунта, то деформация грунтов будет уже пластической, т.е. не восстанавливаемой со временем даже после снятия нагрузки (например, сноса здания) и приведет к существенному изменению структуры грунтов (как минимум тех, которые находятся ближе всего к подошве фундамента). Такая деформация называется просадкой и будет она значительно больше чем осадка, вот только рассчитать просадку из-за пластической деформации даже приблизительно не возьмется никто (просадка при замачивании просадочных грунтов и по другим возможным причинам, здесь не рассматривается).
Методы уплотнения грунтов перед началом строительства здесь также не рассматриваются. Тем не менее уплотнение грунта перед началом устройства фундамента позволит уменьшить итоговую осадку основания, определить которую мы и собираемся.
Основные положения, принимаемые при расчете осадки основания:
1.
Теоретически для расчета осадки основания достаточно просто знать закон Гука, согласно которому
σ = ЕΔh/h или Δh = σh/E (391.1)
где σ - нормальное напряжение, действующее на стержень, измеряемое в МПа или кгс/см2.
Примечание: нормальные напряжения при рассмотрении оснований часто называются вертикальными нормальными, а потом и просто вертикальными. Сути дела это не меняет, однако позволяет лучше представить направление действия напряжений.
Е - модуль упругости стержня, также измеряемый в МПа или кгс/см2, h - высота (длина) стержня,Δh - величина деформации стержня, которую можно было бы рассматривать как осадку основания, если бы мы действительно имели под подошвой фундамента некий стержень конечной длины и постоянного по длине сечения. Вместо это у нас под фундаментом весь земной шар, состоящий из множества пород, слоев грунтов, грунтовых вод и пр. Поэтому:
2.
При расчете осадки основания используется модель линейно деформируемого полупространства под подошвой фундамента.
3.
В этом линейно деформируемом полупространстве давление фундамента на основание будет чем глубже, тем меньше из-за перераспределения напряжений на единицу площади по мере заглубления. Однако зависимость между глубиной и распределением напряжения - не линейная. Например для точечного фундамента с достаточно малой площадью подошвы давление на основание можно условно рассматривать как сосредоточенную нагрузку в вершине конуса. И чем больше высота конуса, тем больше площадь, на которую будет распределяться эта нагрузка. Таким образом конус - это как бы и есть деформируемый стержень переменного сечения. Давление фундамента на основание обозначается как σq и определяется, как дополнительное вертикальное напряжение. На рассматриваемой глубине z это напряжение обозначается как σzq (см. рисунок 391.1)
Примечание: в СНиПе 2.02.01-83 нагрузка на основание обозначается литерой р, в теоретической механике нагрузка чаще обозначается литерой q и мне такое обозначение ближе. Впрочем принципиального значения это не имеет.
4.
Помимо давления от фундамента на нижележащие слои грунтов давят вышележащие слои грунтов. Это давление обозначается как σγ и определяется, как вертикальное напряжение от собственного веса грунта. Предполагается, что вертикальное напряжение от собственного веса грунта прямо пропорционально рассматриваемой глубине и объемному весу грунта
σγ = γh
где γ - объемный вес сжимаемого грунта, находящегося ниже подошвы фундамента, h - высота слоя сжимаемого грунта
Примечание: В СНиПе 2.02.01-83 это давление обозначается как σg, в СП 50-101-2004 - как σγ, но опять же принципиального значения это не имеет. Мне больше нравится обозначение σγ.
5.
Так как по мере заглубления вертикальные напряжения от фундамента уменьшаются, а от вышележащих слоев грунта увеличиваются, то соответственно и деформации, вызываемые этими напряжениями, изменяются. Т.е. чем глубже, тем меньше будет влияние нагрузки от фундамента на осадку основания, к тому же на больших глубинах основание и так уже осело под постоянно действующей нагрузкой от вышележащих грунтов, конечно в том случае, если эти грунты находятся в таком состоянии достаточно давно, желательно тысячи или даже миллионы лет. Таким образом нет необходимости рассматривать толщу грунтов бесконечно большой высоты. Нижняя граница сжимаемой толщи принимается на глубине z = Hc, где выполняется условие σzq = 0.2σzγ (см. рис. 391.1).
Примечание: если нижняя граница сжимаемой толщи находится в грунте с модулем деформации Е < 5 МПа (50 кгс/см2) или такой слой залегает непосредственно ниже определенной глубины z = Hc, то нижняя граница сжимаемого слоя определяется, исходя из условия σzq = 0.1σzγ.
При этом изменение значения вертикальных напряжений в зависимости от глубины принимается согласно следующей расчетной схеме:
 Рисунок 391.1 Схема распределения вертикальных напряжений в линейно-деформируемом полупространстве
Здесь
DL - отметка планировки (уровень грунта после окончания строительства);
NL - отметка поверхности природного рельефа (уровень грунта до начала строительства);
FL - отметка подошвы фундамента;
WL - уровень подземных вод;
В.С - нижняя граница сжимаемой толщи, определяемая расчетом;
d и dn глубина заложения фундамента соответственно от уровня планировки и от поверхности природного рельефа;
b - ширина фундамента;
q - среднее давление под подошвой фундамента;
q0 - дополнительное давление на основание;
σzγ и σzγ,0 - вертикальное напряжение от собственного веса грунта на глубине z от подошвы фундамента и на уровне подошвы;
σzq и σzq,0 - дополнительное вертикальное напряжение от внешней нагрузки на глубине z от подошвы фундамента и на уровне подошвы;
Нс - глубина сжимаемой толщи, определяемая расчетом.
6.
Так как на значение дополнительного вертикального напряжения кроме рассматриваемой в п.3 глубины также влияет ширина фундамента и рассматриваемая точка подошвы фундамента, то значение нагрузки от фундамента на рассматриваемой глубине z рекомендуется определять по следующим формулам:
σzq= aqo (391.2.1)
σzq,c = aqo/4 (391.2.2)
где
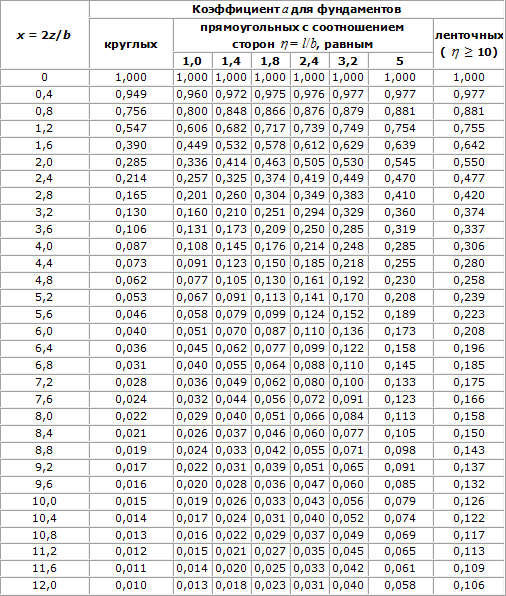
а - коэффициент, принимаемый по таблице 391.1 в зависимости от формы подошвы фундамента, соотношения сторон прямоугольного фундамента и относительной глубины, равной: x = 2z/b при определении σzq и x = z/b при определении σzq,c. Приведенные в таблице 391.1 значения коэффициента а - результат достаточно сложных расчетов для модели линейно деформируемого полупространства, что позволяет проектировщику сэкономить множество времени, сил и вообще значительно упростить расчет (хотя поначалу так не кажется).
Таблица 391.1
Рисунок 391.1 Схема распределения вертикальных напряжений в линейно-деформируемом полупространстве
Здесь
DL - отметка планировки (уровень грунта после окончания строительства);
NL - отметка поверхности природного рельефа (уровень грунта до начала строительства);
FL - отметка подошвы фундамента;
WL - уровень подземных вод;
В.С - нижняя граница сжимаемой толщи, определяемая расчетом;
d и dn глубина заложения фундамента соответственно от уровня планировки и от поверхности природного рельефа;
b - ширина фундамента;
q - среднее давление под подошвой фундамента;
q0 - дополнительное давление на основание;
σzγ и σzγ,0 - вертикальное напряжение от собственного веса грунта на глубине z от подошвы фундамента и на уровне подошвы;
σzq и σzq,0 - дополнительное вертикальное напряжение от внешней нагрузки на глубине z от подошвы фундамента и на уровне подошвы;
Нс - глубина сжимаемой толщи, определяемая расчетом.
6.
Так как на значение дополнительного вертикального напряжения кроме рассматриваемой в п.3 глубины также влияет ширина фундамента и рассматриваемая точка подошвы фундамента, то значение нагрузки от фундамента на рассматриваемой глубине z рекомендуется определять по следующим формулам:
σzq= aqo (391.2.1)
σzq,c = aqo/4 (391.2.2)
где
а - коэффициент, принимаемый по таблице 391.1 в зависимости от формы подошвы фундамента, соотношения сторон прямоугольного фундамента и относительной глубины, равной: x = 2z/b при определении σzq и x = z/b при определении σzq,c. Приведенные в таблице 391.1 значения коэффициента а - результат достаточно сложных расчетов для модели линейно деформируемого полупространства, что позволяет проектировщику сэкономить множество времени, сил и вообще значительно упростить расчет (хотя поначалу так не кажется).
Таблица 391.1
 qo = q - σzγ,0 - дополнительное вертикальное давление на основание (для фундаментов шириной b ≥ 10 м принимается q0 = q)
q - среднее давление под подошвой фундамента (среднее потому, что в зависимости от формы фундамент может рассматриваться как балка на упругом основании и для такой балки распределение давления по ширине подошвы может быть не равномерным. Таким образом принятие среднего значения также позволяет упростить расчеты).
szγ,0 - вертикальное напряжение от собственного веса грунта на уровне подошвы фундамента. При планировке срезкой принимается σzγ,0 = γ'd (в данном случае следует помнить, что рисунок 391.1 является схематическим и отметка поверхности рельефа может быть выше отметки планировки, а не ниже, как показано на рисунке), при отсутствии планировки и планировке подсыпкой σzγ,0 = γ'dn, где γ' - удельный вес грунта, расположенного выше подошвы фундамента, d и dn - показаны на рис.391.1.
Примечания к таблице 391.1:
1. b - ширина или диаметр фундамента, l - длина фундамента.
2. Для фундаментов, имеющих подошву в форме правильного многоугольника с площадью F, значения a принимаются как для круглых фундаментов радиусом r = √F/п.
3. Для промежуточных значений x и η коэффициент a определяется по интерполяции.
7.
Согласно вышеизложенному определение значения дополнительного вертикального напряжения в начале и конце рассматриваемого слоя грунта не представляет большой проблемы и в итоге определение осадки s выполняется методом послойного суммирования по следующей формуле:
qo = q - σzγ,0 - дополнительное вертикальное давление на основание (для фундаментов шириной b ≥ 10 м принимается q0 = q)
q - среднее давление под подошвой фундамента (среднее потому, что в зависимости от формы фундамент может рассматриваться как балка на упругом основании и для такой балки распределение давления по ширине подошвы может быть не равномерным. Таким образом принятие среднего значения также позволяет упростить расчеты).
szγ,0 - вертикальное напряжение от собственного веса грунта на уровне подошвы фундамента. При планировке срезкой принимается σzγ,0 = γ'd (в данном случае следует помнить, что рисунок 391.1 является схематическим и отметка поверхности рельефа может быть выше отметки планировки, а не ниже, как показано на рисунке), при отсутствии планировки и планировке подсыпкой σzγ,0 = γ'dn, где γ' - удельный вес грунта, расположенного выше подошвы фундамента, d и dn - показаны на рис.391.1.
Примечания к таблице 391.1:
1. b - ширина или диаметр фундамента, l - длина фундамента.
2. Для фундаментов, имеющих подошву в форме правильного многоугольника с площадью F, значения a принимаются как для круглых фундаментов радиусом r = √F/п.
3. Для промежуточных значений x и η коэффициент a определяется по интерполяции.
7.
Согласно вышеизложенному определение значения дополнительного вертикального напряжения в начале и конце рассматриваемого слоя грунта не представляет большой проблемы и в итоге определение осадки s выполняется методом послойного суммирования по следующей формуле:
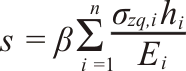 (391.3)
где
β - безразмерный коэффициент, принимаемый равным 0.8.
σzq,i - среднее значение дополнительного вертикального нормального напряжения в i-м слое грунта, равное полусумме указанных напряжений на верхней zi-1 и нижней zi границах слоя по вертикали, проходящей через центр подошвы фундамента.
hi и Еi - соответственно высота и модуль упругости i-го слоя грунта.
n - количество рассматриваемых слоев основания.
8.
Чтобы определить высоту сжимаемого слоя грунта Нс, как правило составляется таблица, в которую вносятся значения дополнительного вертикального напряжения и напряжения от собственного веса грунта в начале и в конце рассматриваемого слоя (пример составления подобной таблицы приводится отдельно).
9.
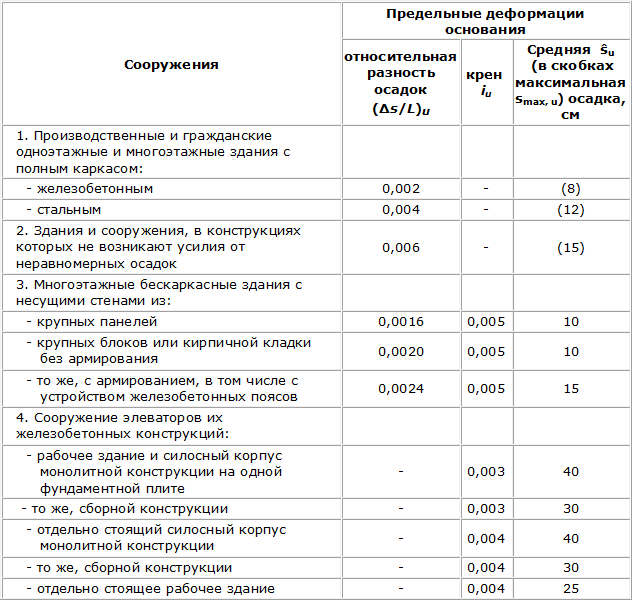
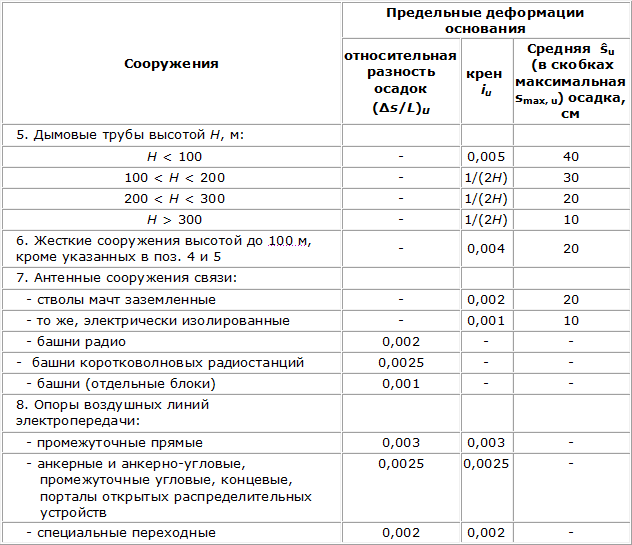
Суммарная осадка, определенная по формуле 391.3, не должна превышать предельных значений, приведенных в таблице 391.2, т.е s ≤ šu:
Таблица 391.2 (391.3)
где
β - безразмерный коэффициент, принимаемый равным 0.8.
σzq,i - среднее значение дополнительного вертикального нормального напряжения в i-м слое грунта, равное полусумме указанных напряжений на верхней zi-1 и нижней zi границах слоя по вертикали, проходящей через центр подошвы фундамента.
hi и Еi - соответственно высота и модуль упругости i-го слоя грунта.
n - количество рассматриваемых слоев основания.
8.
Чтобы определить высоту сжимаемого слоя грунта Нс, как правило составляется таблица, в которую вносятся значения дополнительного вертикального напряжения и напряжения от собственного веса грунта в начале и в конце рассматриваемого слоя (пример составления подобной таблицы приводится отдельно).
9.
Суммарная осадка, определенная по формуле 391.3, не должна превышать предельных значений, приведенных в таблице 391.2, т.е s ≤ šu:
Таблица 391.2
 Вот в принципе и все основные положения, принимаемые при расчете осадки основания (и соответственно фундамента дома). Пример практического использования этих достаточно абстрактных формул и положений приводится отдельно.
Вот в принципе и все основные положения, принимаемые при расчете осадки основания (и соответственно фундамента дома). Пример практического использования этих достаточно абстрактных формул и положений приводится отдельно.
|
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|