Тема: Использование производной для нахождения наилучшего решения в прикладных задачах

Стр 1 из 2Следующая ⇒

Тема: Использование производной для нахождения наилучшего решения в прикладных задачах

Краткое изложение темы.

Примеры выполнения заданий.

Пример 1.

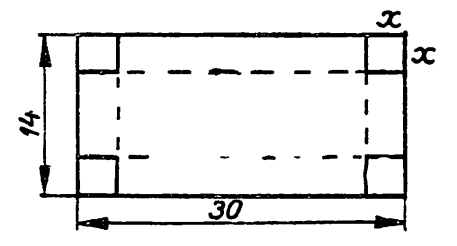
Пример 2.

Найти длины сторон прямоугольника с периметром 20см, имеющего наименьшую диагональ.

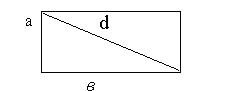
Решение:

Пусть а и в длины сторон прямоугольника, d - его диагональ. Тогда a+b=10. По теореме Пифагора d²=a²+b². По условию задачи a>0,b>0. b=10-a>0, значит 0 <a< 10.

d²=a²+(10-a)²=2a²-20a+100, 0<a< 10.

Таким образом, задача свелась к нахождению такого значения а, при котором функция d(a)=2a²-20a+100 принимает наименьшее значение на интервале 0 < a <10.

Найдем производную d'(a)=4a-20.

Критическая точка .

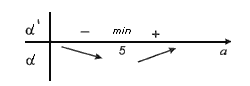
a=5 точка минимума. Следовательно, наименьшее значение функция d(a) на интервале (0;10) принимает в точке a=5. При этом b=5.

Прямоугольник с равными сторонами называется квадратом.

Ответ: наименьшая диагональ у квадрата со стороной 5см.

Пример 3.

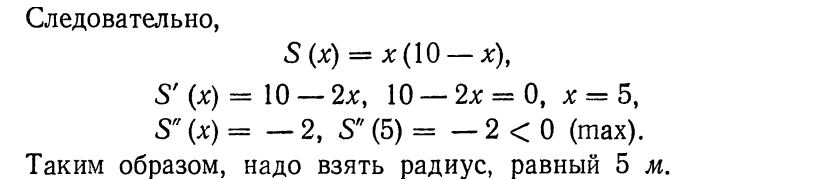
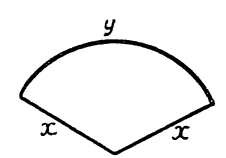
Ответ: площадь клумбы будет наибольшей, если радиус круга возьмем 5м.

12 Следующая ⇒