Контакты

Случайная статья

Повторение. Производная функции.

Повторение. Производная функции.

1. Теоретический материал.

Определение. Производной функции в точке Х₀ называется число, к которому стремится разностное отношение f^’(X₀) = 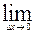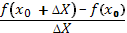при Х, стремящемся к нулю.

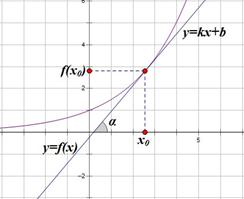
Определение. Производная с геометрической точки зрения - это угловой коэффициент касательной k = = = .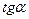

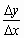Определение. Производная с физической точки зрения – это мгновенная скорость в момент времени t.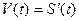

Правила дифференцирования:

Формулы дифференцирования

ДОМА:

Самостоятельная работа по теме

«Производная функции. Физический и геометрический смысл производной».

1. Точка движется прямолинейно по закону S (t)= 2t³ – 0,5t² + 3t (S – путь в метрах, t – время в секундах). Вычислить скорость движения точки в момент времени t=1с.

2. Найти угловой коэффициент касательной, проведенной к графику функции

у = 3х³ – 2х + 1 в его точке с абсциссой х₀ = 1.

3. Найти производную сложной функции: f(x)= (3 – 2х)³.

4. Напишите уравнение касательной к графику функции 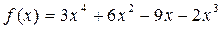в точке .

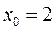5. Прямолинейное движение точки описывается законом 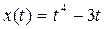. Найдите ускорение в момент времени t=1.

6. Найдите тангенс угла наклона касательной к графику функции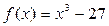

в точке пересечения этого графика с осью абсцисс.

Выполните тест по теме «Производная функции».

Вариант 1.

А1.Найти производную функции .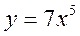

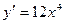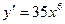1) 2) 3)

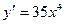
А2. Найти производную функции .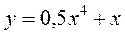

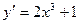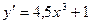1) 2) 3)

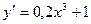
А3. Найти производную функции .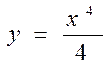

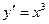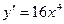1) 2) 3)

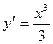
А4. Найти производную функции .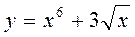

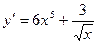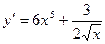1) 2) 3)

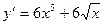
А5. Найти производную функции.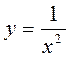

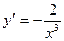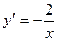1) 2) 3)

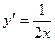
Вариант 2.

А1.Найти производную функции .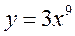

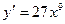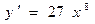1) 2) 3)

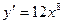
А2. Найти производную функции .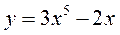

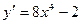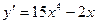1) 2) 3)

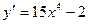
А3. Найти производную функции .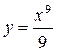

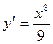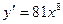1) 2) 3)

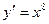
А4. Найти производную функции .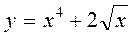

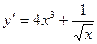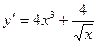1) 2) 3)

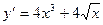
А5. Найти производную функции.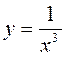

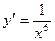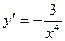1) 2) 3)

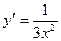
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.