
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Решение задач прикладного характера.
Решение задач прикладного характера.
Решение прямоугольных треугольников
Дидактическая цель.Научиться использовать вычислительные средства при решении задач прикладного характера..
Основные знания и умения.Иметь представления о решении прикладных задач с помощью вычислительных средств.
Мотивация познавательной деятельности.Применение знаний и умений использовать таблицы и микрокалькуляторы при решении задач прикладного характера помогает показать использование математики в различных отраслях науки и техники.
Повторение опорных знаний.Повторить основные соотношения в прямоугольном треугольнике (рис. 3): Вставить пропущенные формулы.!
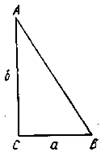 1)
1) 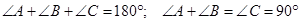
2) 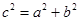 ;
;
3) sin A= ?
4) cosA=?
5) tg A=?
6) sin B=?
7) cosB=?
8) tg B=?
9) 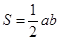 . Рис. 3
. Рис. 3
Задание! Из формул с № 2-8 в блокноте выразить катет а, катет в, гипотенузу с.
Обобщение и систематизация знаний.При выполнении задач па решение прямоугольных треугольников нужно учитывать, что использование результатов промежуточных действий ведет к потере: точности вычислений. Основные случаи решения прямоугольных треугольников показаны в табл. 5.
Применение знаний при решении типовых примеров и задач.
Решить задачи с использованием микрокалькулятора и математических таблиц.
1. Решить прямоугольный треугольник:
а) Дано: 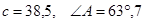 . Найти: ÐВ, а, b.
. Найти: ÐВ, а, b.
б) Дано: с = 0,675, а = 0,212. Найти: ÐA, ÐB, b.
в) Дано: а = 28,4, b = 18,6. Найти: ÐA, ÐB, с.
г) Дано: а = 635, ÐВ = 54°,7. Найти: ÐА, b, с.
Таблица 5
| Дано | Найти | Решение |
| 1. с, А (рис. 4) | B, a, b | ÐB = 90° – ÐA; a = c sin A; b = c cos A |
| 2. а, А (рис. 5) | B, b, c | ÐB = 90° – ÐA; b = a ctg A; c = 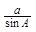
|
| 3. а, b (рис. 6) | A, B. c | c = 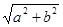 ; tg B = ; tg B = 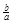 ; ÐB – по таблицам; ÐA = 90° – ÐB ; ÐB – по таблицам; ÐA = 90° – ÐB
|
| 4. а, с (рис. 7) | A, B, b | b = 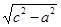 ; sin A = ; sin A = 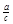 ; ÐA – по таблицам; ÐB = 90° – ÐA ; ÐA – по таблицам; ÐB = 90° – ÐA
|
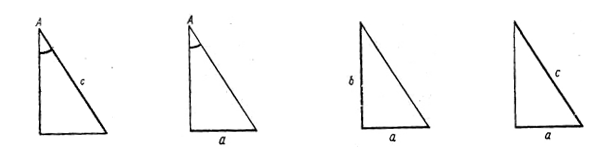
Рис. 4 Рис. 5 Рис. 6 Рис. 7
2. Горная железная дорога на одном из участков поднимается на 1 м на каждые 60 м пути. Найти угол подъема дороги на данном участке.
3. Насыпь, поперечное сечение которой есть равнобедренная трапеция, имеет у основания ширину 12 м. Высота насыпи 3 м. Определить ширину верхней части насыпи, если при ее постройке откос составлял 39°.
Домашнее задание.
1. Решить прямоугольный треугольник по катету и острому углу: b = 8,35, ÐA =
= 58°,2.
2. Решить прямоугольный треугольник по двум катетам: а = 264, b = 535.
3. Решить прямоугольный треугольник по гипотенузе и острому углу: с = 36,5,
ÐА = 62°,6.
3. Вычислить по таблицам:
а) 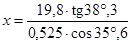 ; б)
; б) 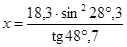 ; в)
; в) 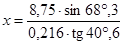
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|