Порядок решения задач с использованием принципа Даламбера

⇐ ПредыдущаяСтр 2 из 3Следующая ⇒

Порядок решения задач с использованием принципа Даламбера

1. Составить расчетную схему.

2. Выбрать систему координат.

3. Выяснить направление и величину ускорения.

4. Условно приложить силу инерции.

5. Составить систему уравнений равновесия.

6. Определить неизвестные величины.

Примеры решений задач

Пример 1.Рассмотрим движение платформы по шероховатой поверхности с ускорением (рис. 14.4).

Решение

Активные силы: движущая сила, сила трения, сила тяжести. Реакция в опоре R. Прикладываем силу инерции в обратную от ускорения сторону. По принципу Даламбера, система сил, действующих на платформу, становится уравновешенной, и можно составить уравнения равновесия. Наносим систему координат и составляем уравнения проекций сил.

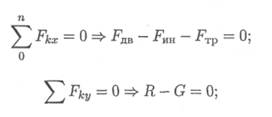
Тема 1.13. Движение материальной точки 103

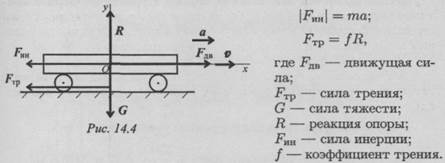
Пример 2.Тело весом 3500 Н движется вверх по наклонной плоскости согласно уравнению S = 0,16t² (рис. 14.5). Определить величину движущей силы, если коэффициент трения тела о плоскость f = 0,15.

Решение

1. Составим расчетную схему, выберем систему координат с осью
Ох вдоль наклонной плоскости.

Активные силы: движущая, сила трения, сила тяжести. Наносим реакцию в опоре перпендикулярно плоскости. Чтобы верно направить силу инерции, необходимо знать направление ускорения, определить это можно по уравнению движения.

При а > 0 движение равноускоренное.

2.Определяем ускорение движения: а = v' = S"; v = S' = 0,32t; а = v' = 0,32 м/с² > 0.

Силу F_ин направим в обратную от ускорения сторону.

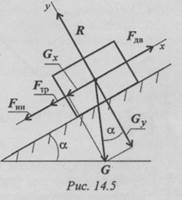
3.По принципу Даламбера составим уравнения равновесия:

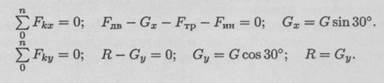Лекция 14

4. Подставим все известные величины в уравнения равновесия:

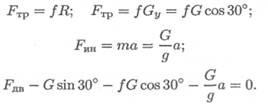
Выразим неизвестную силу и решим уравнение:

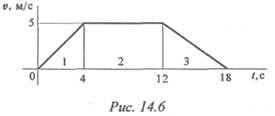
Пример 3.График изменения скорости лифта при подъеме известен (рис. 14.6). Масса лифта с грузом 2800 кг. Определить натяжение каната, на котором подвешен лифт на всех участках подъема.

⇐ Предыдущая 123 Следующая ⇒