Тема: Применение производной функции. Решение задач.

Тема: Применение производной функции. Решение задач.

Дата: 07.10.2020 г.

Группа: МОЦИ-258

Студенты должны знать: понятие «производной», правила нахождения производных.

Студенты должны уметь:решать задачи на вычисление производных; уметь составлять уравнение касательной

Актуализация знаний студентов

Пример №3

Найти производную функции:

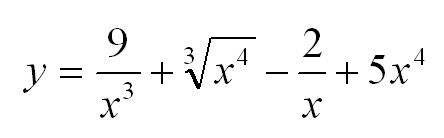
Решение:

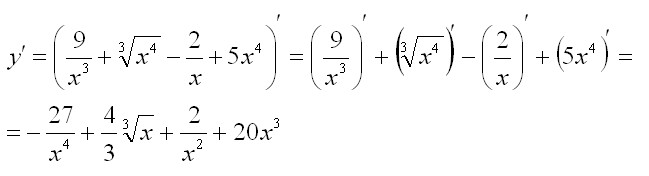
Пример 4

Функция 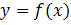определена на промежутке 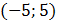. На рисунке изображен график ее производной 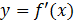(см. рис.5). К графику функции провели все касательные, параллельные прямой 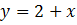. Найти наименьшую из абсцисс точек, в которых проведены эти касательные.

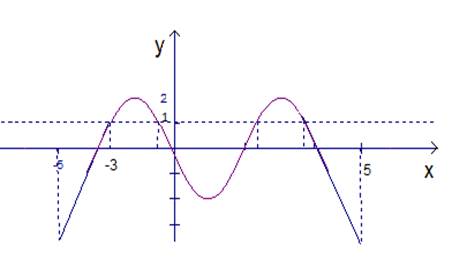рис.5

Решение.

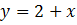Поскольку дан график производной функции, то в каждой точке известен тангенс угла наклона касательной. Все касательные параллельны прямой , в которой 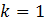- угловой коэффициент.

Значит, 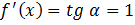. Проведем прямую 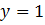, и найдем точку с наименьшей абсциссой.

Важно понимать, что на графике изображена не сама функция, а ее производная. Если дана производная, то известен тангенс угла наклона в каждой точке.

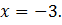Ответ:

Домашнее задание:

1) Найти производную функций:

а) y=x³−2x²+7x−1; б) y=sinx−ln3x;

в) y=(3x−1)⋅5^x; г) y=lnsin3x

Критерии оценивания:

Оценка «отлично»- выставляется обучающемуся, если правильно решены все задания, выполнены в полной мере, изложены логично.

Оценка «хорошо»- выставляется обучающемуся, если допущены незначительные погрешности в задании.

Оценка «удовлетворительно»- выставляется обучающемуся, если ответ на вопрос нелогичный, не полный.

Оценка «неудовлетворительно»- выставляется обучающемуся, если задания не решены.

ВНИМАНИЕ!!!

Уважаемые студенты, практическое задание необходимо выполнить в рабочей тетради (сфотографировать) или в формате Документа Word. Отправлять для проверки в личные сообщения на страницу ВКонтакте: https://vk.com/kolomiyetssg?z=photo95751036_324720501%2Falbum95751036_0%2Frev

Преподаватель: Коломиец Светлана Григорьевна