Площадь поверхности цилиндра. S = 2πR2 + 2πRH = 2πR(R + H).. V = Sосн *Н = πR2Н.

24.03.2020

Группа 711 Урок 3

Тема урока: Цилиндр и конус. Усеченный конус. Основание, высота, боковая поверхность, образующая, развертка.

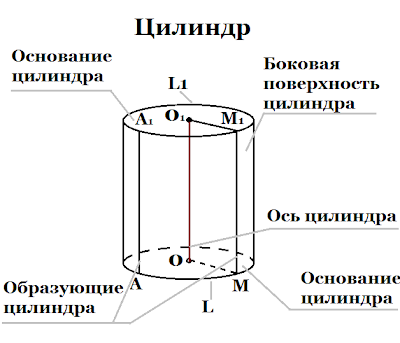
У цилиндра есть два основания (верхнее и нижнее) и оба они имеют форму окружности. Перпендикулярная к основаниям плоскость, называется боковой поверхностью цилиндра.

Возьмите лист бумаги и соедините его противоположные края – Вы как раз получите боковую поверхность цилиндра. А что будет, если этот лист снова развернуть? Он снова будет иметь форму прямоугольника. Это значит, что боковая поверхность цилиндра – это прямоугольная плоскость.

Площадь поверхности цилиндра

Найти площадь оснований можно по следующей формуле: S = 2πR².

Для тех, кто хорошо выучил тему об окружностях, возразят, что в формуле не должно быть цифры «2», однако из-за того, что основания в виде окружности два, и они равны между собой, площадь достаточно умножить на «2».

А теперь перейдем к площади поверхности. Как говорилось ранее, боковая поверхность создана прямоугольником, поэтому достаточно умножить длину его на ширину. Ширина – это высота цилиндра, а длина – это длина окружности, поэтому площадь боковой поверхности:

S = 2πRH.

А значит, общая площадь поверхности цилиндра:

S = 2πR2 + 2πRH = 2πR(R + H).

Объем цилиндра:

V = Sосн *Н = πR2Н.

КОНУС

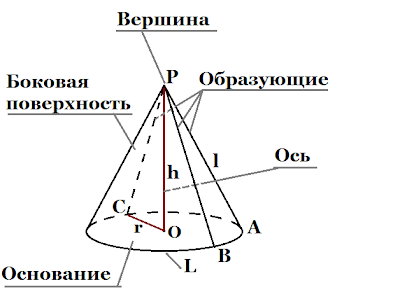
Конус – это тело, которой состоит из окружности, которая находится в основании, из точки равноудаленной от всех точек на окружности, а также от прямых, соединяющих эту точку (вершину) со всеми точками, лежащими на окружности.

Несколькими вопросами ранее, мы рассматривали пирамиду. Так вот конус – это частный случай пирамиды, в основании которой лежит окружность. Практически все свойства пирамиды подходят и для конуса.

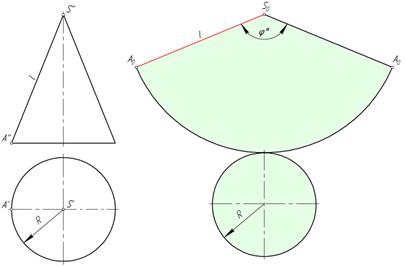
Образующие конуса– это отрезки, заключенные между точками окружности и вершиной конуса. Образующие конуса равны между собой.

Чтобы найти длину образующей, следует воспользоваться формулой:

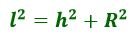
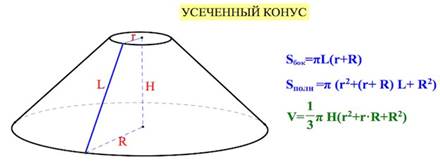
Если все образующие соединить между собой, можно получить боковую поверхность конуса. Общая его поверхность состоит из боковой поверхности и основания в виде окружности.

Конус имеет высоту. Чтобы ее получить, достаточно опустить перпендикуляр из вершины, непосредственно, в центр основания.

Чтобы найти площадь боковой поверхности, следует воспользоваться формулой:

Для нахождения полной площади поверхности конуса воспользуйтесь следующей формулой:

Формула объема конуса похожа на объем цилиндра, но разделенная на «3»:

Развертки: Цилиндр

Конус

Усечённый конус

Задание для самостоятельной работы:

Создать модель цилиндра, конуса или усеченного конуса (одну на выбор).