Правильные многогранники. все его грани — равные правильные многоугольники;. в каждой его вершине сходится одно и то же число рёбер.

Правильные многогранники

Выпуклый многогранник называется правильным, если:

1. все его грани — равные правильные многоугольники;

2. в каждой его вершине сходится одно и то же число рёбер.

Все рёбра правильного многогранника равны, а также равны все двугранные углы, содержащие две грани с общим ребром.

Возникают вопросы:

1. какие правильные многоугольники могут быть гранями правильного многогранника?

2. Сколько граней может иметь правильный многогранник?

Не существует правильного многогранника, гранями которого являются правильные многоугольники, если число их сторон 6 или больше, то есть правильные n-угольники, если n≥6.

1. У правильного n-угольника, если n≥6, углы не меньше 120°.

2. В каждой вершине многогранника должно быть не меньше трёх углов.

3. Даже при трёх углах сумма всех углов уже достигает 360°.

4. Сумма всех плоских углов при каждой вершине выпуклого многогранника меньше 360°.

Следовательно, не существует правильного многогранника, гранями которого являлись бы правильные n-угольники, если n≥6.

Только правильные треугольники, четырёхугольники (квадраты) и пятиугольники могут быть гранями правильного многогранника.

Существуют ли правильные многогранники с такими гранями, и сколько граней они имеют? Очевидно, меньшее возможное число граней — четыре.

Существующие правильные многогранники

тетраэдрс 4 гранями, 6 рёбрами и 4 вершинами:

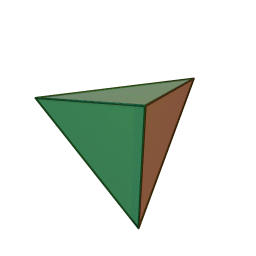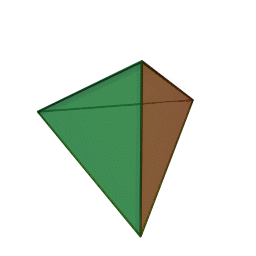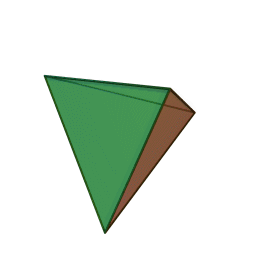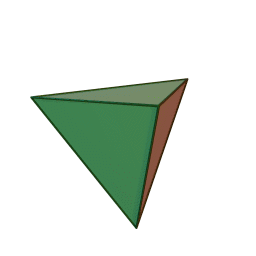
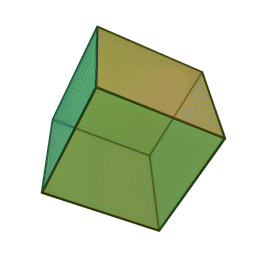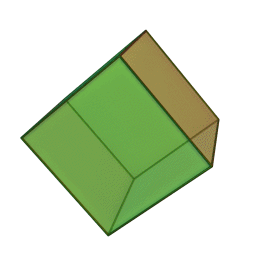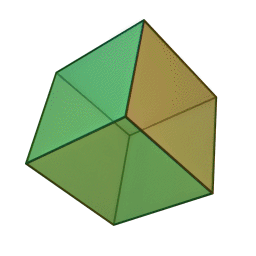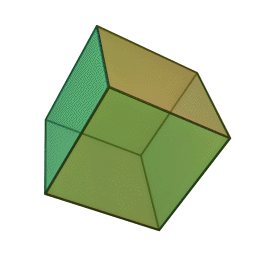
кубс 6 гранями, 12 рёбрами и 8 вершинами:

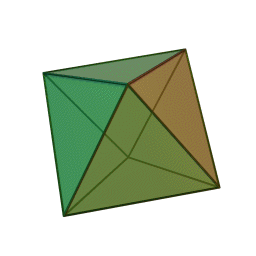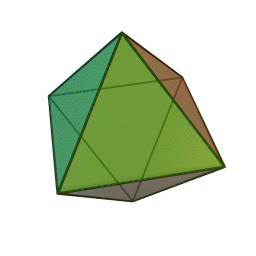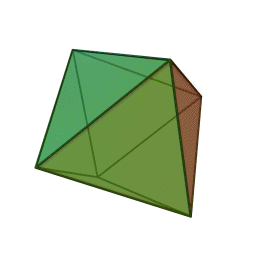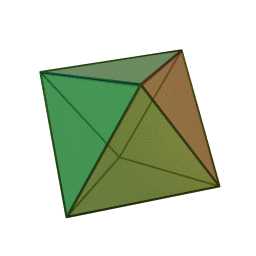
октаэдр с 8 гранями, 12 рёбрами и 6 вершинами:

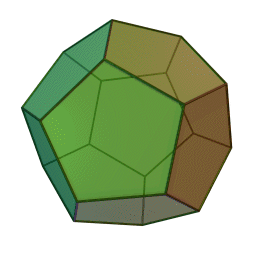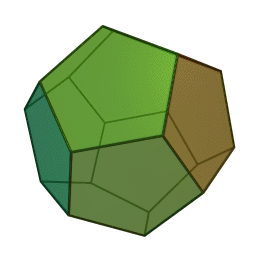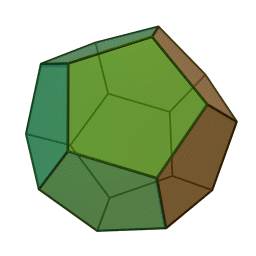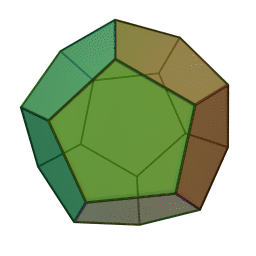
додекаэдр с 12 гранями, 30 рёбрами и 20 вершинами:

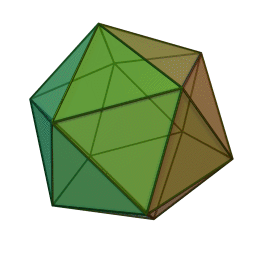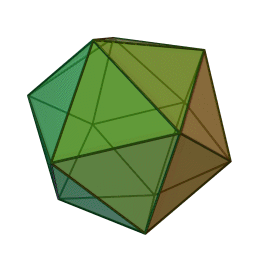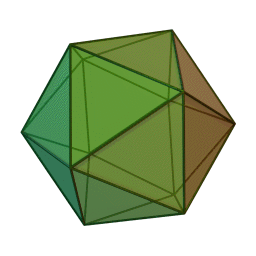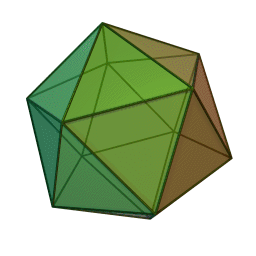
икосаэдр с 20 гранями, 30 рёбрами и 12 вершинами: