Контакты

Случайная статья

Урок: Понятие степени с целым отрицательным показателем

Урок: Понятие степени с целым отрицательным показателем

1. Вспомним материал 7 класса:

Определение: Степень числаaс натуральным показателемn - это выражение вида aⁿ, значение которого равно произведению n множителей, каждый из которых равен a, то есть, .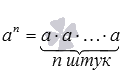
В частности, степенью числа a с показателем 1 называется само число a, то есть, a¹=a.

Вы это хорошо знаете, поэтому такие примеры легко посчитаете устно:

а) 2³; б) (–7)²; в) (–3)³; г) ;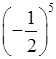

д) 5³; е) 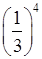; ж) (–2)⁴; з) ;

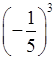и) 6³; к) 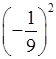; л) (–3)⁰; м) 2¹.

2. Объяснение нового материала.

Определение степени с целым отрицательным показателем:

а^п =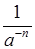

, где а ≠ 0 и n – целое отрицательное число.

Как пользоваться этой записью рассмотрим на примере:

3³ = 27, 3^–3 = .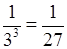

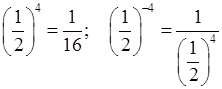= 16.

То есть, мы должны заменить степень с целым показателем дробью, степень в знаменателе уже положительная:

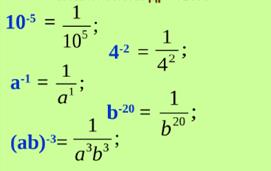
Затем сделать общий вывод: = 1.

Напоминаем, что а⁰ = 1, для а ≠ 0, выражение 0⁰ – не имеет смысла; 0ⁿ = 0 для натуральных п.

Правило: Выражение 0п для целых отрицательных п не имеет смысла.

П р и м е р ы: 12⁰ = 1; (–3,5)⁰ = 1;

0⁴ = 0; 0¹ = 0;

0⁰ – не имеет смысла;

0^–3 – не имеет смысла.

Формирование умений и навыков.

№ 966.

Р е ш е н и е

а) 8 = 2³; 4 = 2²; 2 = 2¹; 1 = 2⁰; 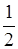= 2^–1; 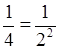= 2^–1; 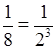= 2^–3.

б) 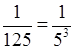= 5^–3; 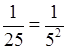= 5^–2; 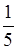= 5^–1; 1 = 5⁰; 5 = 5¹; 25 = 5²;
125 = 5³.

№ 968 (а; б; в; е; з; к).

Р е ш е н и е

а) 4^–2 = ;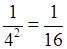

б) (–3)^–3 = ;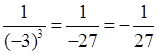

в) (–1)^–9 = 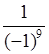= –1;

е) ;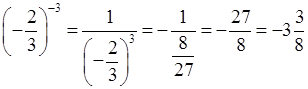

з) ;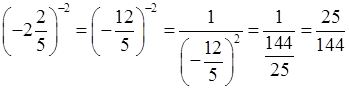

к) 1,125^–1 = .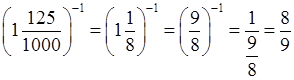

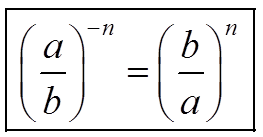
№ 970 (в, г, е).

Р е ш е н и е

в) ;

г) ;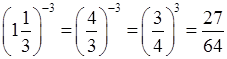

е) .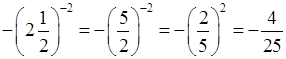

№ 969.

а) –10^–4 = 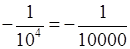= –0,0001;

в) (–0,8)^–2 = ;

д) –(–2)^–3 = .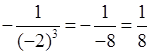

№ 971.

а) 9^–5 = 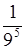> 0;

б) 2,6^–4 = > 0;

в) (–7,1)^–6 = > 0;

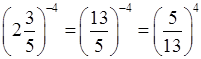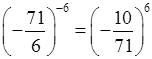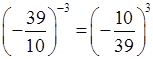г) (–3,9)^–3 = < 0.

Вывод:

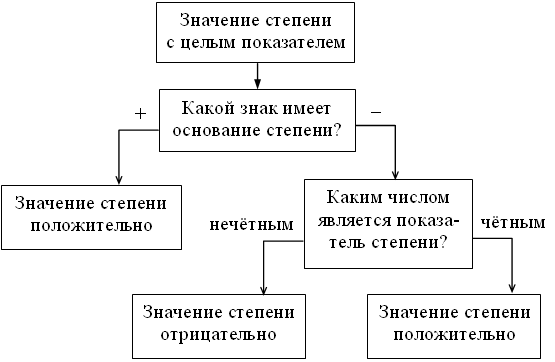
В о п р о с ы у ч а щ и м с я:

– Как определяется степень с целым отрицательным показателем?

– Чему равно любое число (не равное нулю) в нулевой степени?

– Какое значение имеет выражение 0^п при целом n < 0?

– Чему равно а^п · а^–п?

– Можно ли получить отрицательный результат при возведении положительного числа в отрицательную степень?

Домашнее задание:№ 968 (г, д, и), № 969 (б, г, е), № 970 (а, б, д)

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.