Главная Контакты Случайная статья Автоматизация Антропология Археология Архитектура Биология Ботаника Бухгалтерия Военная наука Генетика География Геология Демография Деревообработка Журналистика Зоология Изобретательство Информатика Искусство История Кинематография Компьютеризация Косметика Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Материаловедение Медицина Менеджмент Металлургия Метрология Механика Музыка Науковедение Образование Охрана Труда Педагогика Полиграфия Политология Право Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Электротехника Энергетика
	Мы ввели три основные операции, связанные со скалярными и векторными полями. Это градиент скалярного поля, дивергенция и ротор векторного поля. Можно ли к полученным в результате векторным и скалярным полям применять операции теории поля повторно,и к чему  Мы ввели три основные операции, связанные со скалярными и векторными полями. Это градиент скалярного поля, дивергенция и ротор векторного поля. Можно ли к полученным в результате векторным и скалярным полям применять операции теории поля повторно,и к чему это приведёт? Очевидно, что изначально участвующие объекты должны быть дважды дифференцируемыми, а применение операции осмысленным. Нельзя взять ротор от дивергенции, так как дивергенция-скаляр, а ротор применим только к векторному полю. Удобнее всего повторные операции теории поля представить в виде таблицы:   Скалярное поле U Векторное поле А
	Grad	div	rot
grad		grad div A
div	DU		div rot Aº0
rot	rot grad Uº0		grad div A -D A

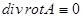       Проверим снача тождество . В силу определения дивергенции и ротора имеем

.

То есть, эта повторная операция может быть истолкована как смешанное произведение векторов-ориентированный объём,который раве нулю, если два вектора, образующих его, совпадают.

DEF 6. Дважды дифференцируемое векторное поле B называется соленоидальным (трубчатым),если .

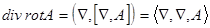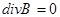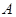Теорема 2. Для того, чтобы поле  было соленоидальным, необходимо и достаточно, чтобы существовало поле A такое,что 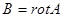.A-называется векторным потенциалом поля /

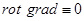       Займёмся теперь тождеством .В силу определения: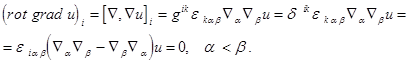

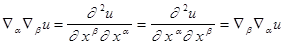Последнее равенство становится понятным,если вспомнить,что

 , так как 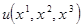-дважды дифференцируемая функция,и,следовательно,смешанные произведения равны.

DEF 7. Дважды дифференцируемое поле А называется потенциальным,если .

Теорема 3. Для того, чтобы векторное поле А было потенциальным,необходимо и достаточно,чтобы существовало скалярное поле  такое,что .

NB.Достаточность в теоремах 2 и 3 следует из приведённых при разборе повторных операций теории поля выкладок. Необходимость является следствием соответствующих теорем из теории уравнений в частных производных.Придётся пока принять это утверждение на веру.Более того,мы приведём без доказательства очень важную теорему,о которой уже упоминали,когда раскладывали тензор второго ранга в сумму симметричного и антисимметричного.

Теорема 4. Любое дважды дифференцируемое векторное поле А представимо в виде суммы потенциального и соленоидального полей:

.

NB.В таблице осталась ещё одна,часто встречающаяся в курсах уравнений в частных производных,формула

.

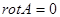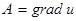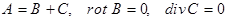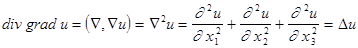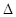-оператор Лапласа, .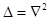