Закон распределения

Закон распределения

Законом распределения случайной величины называется соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями (его можно задать таблично, аналитически (в виде формулы) и графически.

Разобрать пример:

Найти дисперсию случайной величины X, которая задана следующим законом распределения:

Х 2 3 5

p 0,1 0,6 0,3

Решение. По формуле (3.1) находим математическое ожидание:

M (X) = 2*0,1 + 3*0,6 + 5*0,3 = 3,5.

Закон распределения случайной величины X2:

Х2 4 9 25

p 0,1 0,6 0,3

Математическое ожидание М(Х2):

M (X) = 4*0,1 + 9*0,6 + 25*0,3 = 13,3.

По формуле (3.4) находим дисперсию:

D (X) = 13,3 - (3,5)2 = 1,05.

Средним квадратичным отклонением случайной величины Х называется корень квадратный из ее дисперсии: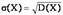

Задания:

1. Возможные значения случайной величины таковы: x₁ = 2, x₂ = 5, x₃ = 8. Известны вероятности первых двух возможных значений: p₁ = 0,4, p₂ = 0,15. Найти вероятность x₃. Математическое ожидание и дисперсию дискретной случайной величины.

2. Найти математическое ожидание и дисперсию дискретной случайной величины, зная ее закон распределения:

Х
p	0,2	0,3	0,5

3. Случайная величина задана законом распределения:

Х
p	0,1	0,5	0,4

Найти среднее квадратичное отклонение этой величины

⇐ Предыдущая 12