Применение производной в экономике швейного предприятия

Применение производной в экономике швейного предприятия

Позвольте предложить вашему вниманию задачу на применение производной экономического содержания, связанную с работой швейного цеха

Вот такую задачу предстоит решить менеджеру швейного производства, арифметические или алгебраические методы не приведут к оптимальному решению. Давайте решать вместе с менеджером!

Обозначим : x – число рабочих мест (или работников); y – число рабочих смен; S – стоимость работы, тогда S = 800x + 6000y + 960xy.

/Здесь 800 x(р) – столько надо заплатить премиальных всем работникам после выполнения задания;

6000 y(р) надо заплатить вспомогательному персоналу за все y смен;

960 xy(р) надо заплатить всем х работникам за выполненное задание в течение y смен./

По условию задачи x∙y = 10∙12 =120 y =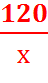

Введём функцию f(x) = S(х) = 800x + 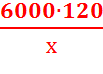+ 960∙120 = 800х + 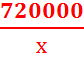+ 115200, где x > 0.

Найдём производную:

f’ (x) = (800x + 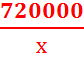+ 115200)’= 800 - = = .

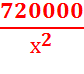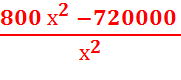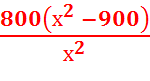Найдём критические точки функции, приравняв производную нулю

f’ (x) = 0, если 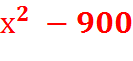= 0, 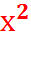= 900, х = 30(берём x > 0).

Проведём исследование функции с помощью производной f’ (x) = где x > 0

Х	0 < Х < 30	Х = 30 Критическая точка	Х > 30
f’(х)	-		+
f (х)	↘ Функция убывает		↗ Функция возрастает
		min

Вывод

• Минимальное значение функция (а значит и сумма выплат) принимает при х = 30, поэтому

необходимо создать 30 рабочих мест и работать в течение четырёх смен (y = 120:30 = 4).

• Вычислим минимальную сумму выплат по формуле S(х) = 800х + 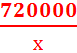+ 115200

S = 800∙30 + 720000:30 + 115200 = 24000 + 24000 + 115200 = 163200(р) –(минимальная)

• Если бы остался прежний бизнес-план, т.е. х = 10, y = 12, то сумма выплат была бы

S = 800∙10 + 720000:10 + 115200 = 8000 + 72000 + 115200 = 195200(р)

• Возьмём любые другие числа х и y, например х = 60, y = 2, тогда

S = 800∙60 + 720000:60 + 115200 = 48000 + 12000 + 115200 = 175200(р)