Лабораторная работа №2. Введение в Фурье-оптику. Линза как оптический процессор. Теория вопроса
Лабораторная работа №2
Введение в Фурье-оптику. Линза как оптический процессор
1. Теория вопроса
В ряде случаев когерентные оптические системы, состоящие из традиционных оптических элементов (линзы, зеркала, и т.д.), можно рассматривать как некие оптические процессоры, осуществляющие определённые математические преобразования, например, преобразование Фурье — преобразование по отношению к функции, определяющей распределение комплексной амплитуды на входе системы. Если для осуществления спектрального разложения функций времени в радиотехнике необходимы сложные резонансные устройства, то пространственные спектры в когерентной оптике получить очень просто. Эту операцию выполняют обычные линзы. Оказывается, что линзы не только могут формировать распределение амплитуд света, соответствующее геометрическому изображению, но и способны создавать Фурье-образ объекта.
Рассмотрим процедуру построения изображения объекта с помощью линзы. Одномерная функция пропускания линзы описывается выражением
(1)
Возьмём для простоты одномерный объект с функцией пропускания  . Полагая, что амплитуда поля волны, падающей на объект, равна единице, на выходе получим распределение поля вида . Полагая, что амплитуда поля волны, падающей на объект, равна единице, на выходе получим распределение поля вида 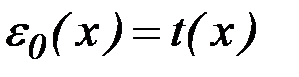 . На расстоянии . На расстоянии   от объекта расположим линзу и построим изображение объекта на произвольном расстоянии от объекта расположим линзу и построим изображение объекта на произвольном расстоянии 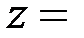 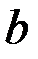 от линзы (рис. 1). от линзы (рис. 1).
Сначала с помощью интеграла Френеля
записанного в одномерной форме, найдем амплитуду светового поля в произвольной точке плоскости на входе линзы:
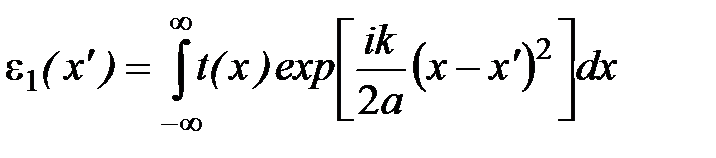 . (3) . (3)
Умножив это выражение на одномерную функцию пропускания линзы, найдём амплитуду поля в той же точке на выходе линзы:
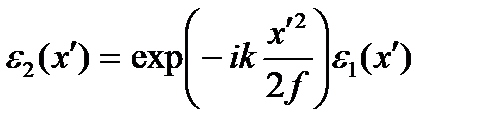 . (4) . (4)
Наконец, амплитуда поля в произвольной точке плоскости, расположенной на расстоянии 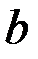 справа от линзы, также описывается соответствующим интегралом Френеля: справа от линзы, также описывается соответствующим интегралом Френеля:
Рис. 1. Схема построения изображения решётки, расположенной в плоскости 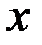 , с помощью линзы, помещённой в плоскости , с помощью линзы, помещённой в плоскости 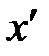 . Справа от линзы на расстоянии . Справа от линзы на расстоянии 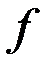 находится фокальная плоскость, на расстоянии находится фокальная плоскость, на расстоянии 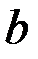 — плоскость изображения — плоскость изображения
| 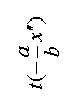
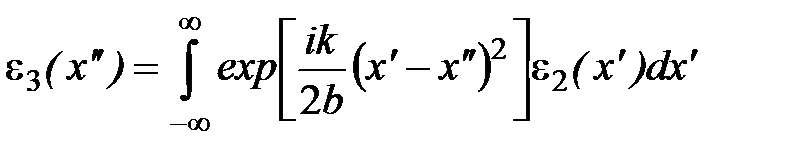 . (5) . (5)
Подставив в (5) выражения для 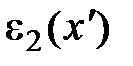 и и 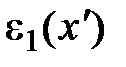 , находим после преобразований , находим после преобразований
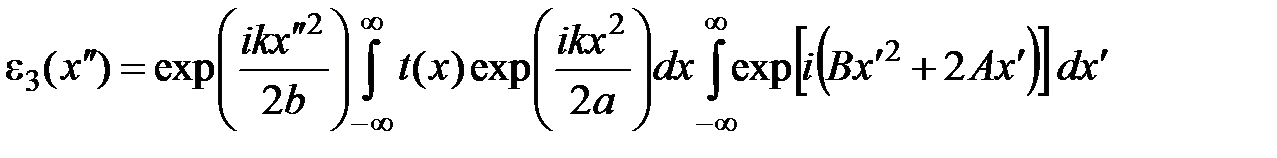 , (6) , (6)
где введены обозначения: 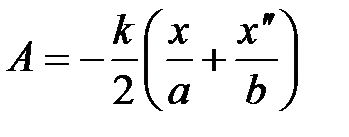 , , 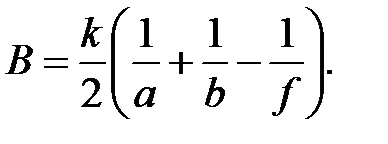 . Последний интеграл в (6) с учётом формулы . Последний интеграл в (6) с учётом формулы

равен 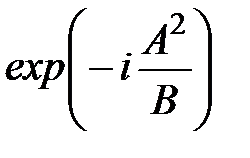 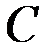 . .
Рассмотрим два случая:
1) Найдём распределение амплитуды поля в задней фокальной плоскости линзы, где 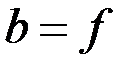 , т.е. , т.е. 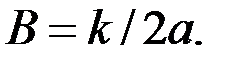 Формула (6) здесь примет вид: Формула (6) здесь примет вид:
 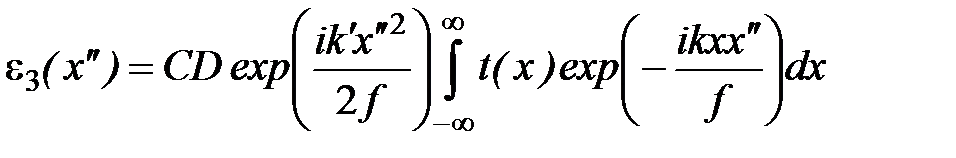 , ,
где 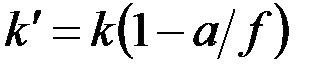 . Отсюда следует, что (с точностью до фазового множителя, не влияющего на распределение интенсивности) в фокальной плоскости линзы формируется Фурье-образ функции пропускания объекта . Отсюда следует, что (с точностью до фазового множителя, не влияющего на распределение интенсивности) в фокальной плоскости линзы формируется Фурье-образ функции пропускания объекта 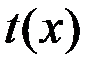 по переменной по переменной 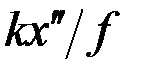 , которая в обычном приближении малых углов дифракции равна поперечной компоненте волнового вектора , которая в обычном приближении малых углов дифракции равна поперечной компоненте волнового вектора 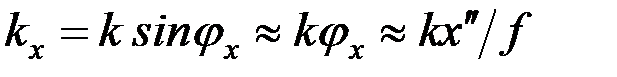 : :
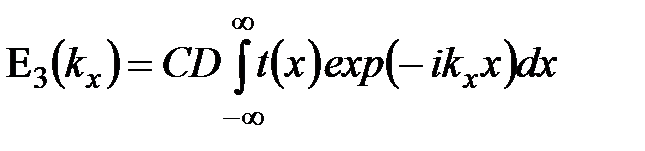 , (7) , (7)
где параметр 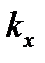 играет роль пространственной частоты. играет роль пространственной частоты.
2) Найдём распределение амплитуды светового поля в плоскости, расстояние которой от линзы 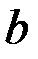 удовлетворяет соотношению: удовлетворяет соотношению:
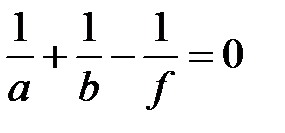 , т.е. , т.е. 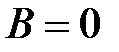 . .
Последний интеграл в (6) можно теперь взять в конечных пределах по апертуре линзы, т. е. по отрезку 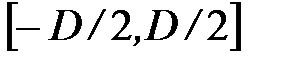 : :
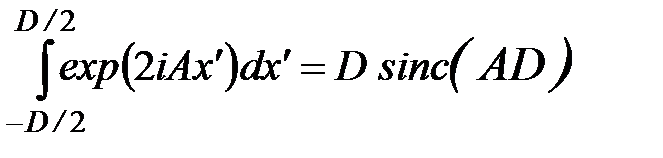 . (8) . (8)
Учитывая, что длина волны мала, по сравнению с размером линзы, можно в этом выражении перейти к пределу
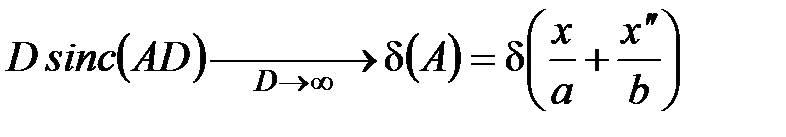 , (9) , (9)
и, подставив в интеграл (6), найти амплитуду светового поля:
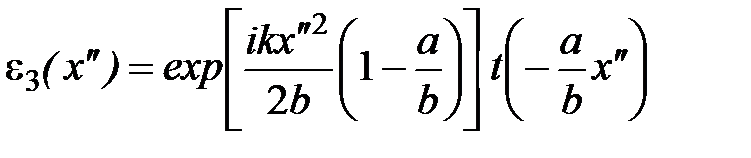 . (10) . (10)
Формула (10) показывает, что распределение амплитуды в данной плоскости с точностью до фазового множителя совпадает с распределением амплитуды в плоскости объекта, задаваемым его функцией пропускания  . Поэтому рассматриваемую плоскость естественно назвать плоскостью изображения объекта («перевёрнутого» вследствие знака «минус» в аргументе функции t), масштаб которого, как видно из (10), увеличился в . Поэтому рассматриваемую плоскость естественно назвать плоскостью изображения объекта («перевёрнутого» вследствие знака «минус» в аргументе функции t), масштаб которого, как видно из (10), увеличился в 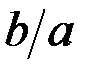 раз. Описанную процедуру построения изображения объекта в виде дифракционной решётки иллюстрирует рис. 1. раз. Описанную процедуру построения изображения объекта в виде дифракционной решётки иллюстрирует рис. 1.
Из формул (8), (9) также видно, что точка с координатой 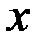 в плоскости объекта переводится линзой в точку с координатой в плоскости объекта переводится линзой в точку с координатой 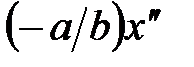 в плоскости изображения только в случае линзы «бесконечно большой», по сравнению с длиной волны. Если же учитывать конечную апертуру линзы, то вместо точки мы получим в плоскости изображение распределения амплитуды светового поля, описываемое функцией в плоскости изображения только в случае линзы «бесконечно большой», по сравнению с длиной волны. Если же учитывать конечную апертуру линзы, то вместо точки мы получим в плоскости изображение распределения амплитуды светового поля, описываемое функцией  , точнее, с учётом круговой формы апертуры, аналогичной формулой, куда вместо функции sin входит специальная функция — функция Бесселя первого порядка от радиальной координаты. При этом структура светового поля вполне аналогична описываемой функцией , точнее, с учётом круговой формы апертуры, аналогичной формулой, куда вместо функции sin входит специальная функция — функция Бесселя первого порядка от радиальной координаты. При этом структура светового поля вполне аналогична описываемой функцией  . Характерный угловой размер получившегося центрального светового пятна определяется формулой . Характерный угловой размер получившегося центрального светового пятна определяется формулой
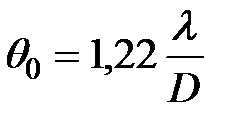
и увеличивается с уменьшением диаметра линзы D. Следовательно, дифракция излучаемой объектом волны на конечной апертуре линзы приводит к «размазыванию» изображения объекта и ухудшению его качества.
Проведённое построение показывает, что формирование линзой изображения объекта, рассматриваемое как дифракционный процесс, можно разделить на два этапа. На первом этапе происходит разложение (анализ) светового поля объекта в Фурье-спектр, который формируется в задней фокальной плоскости линзы. На втором этапе последующее распространение световой волны приводит к восстановлению (синтезу) уже изображения объекта в плоскости изображения. Отсюда следует, что, во-первых, по виду спектра в фокальной плоскости линзы можно установить параметры собственно объекта, во-вторых, воздействуя на спектр объекта, можно управлять параметрами его синтезированного изображения. Помещая в фокальной плоскости линзы диафрагмы, экраны, фазовые объекты, можно осуществить преобразование углового спектра излучения, при котором можно выделить и усилить «полезные» частоты и погасить помехи.
Рассмотрим в качестве примера классический эксперимент Аббе-Портера по пространственной фильтрации, схема которого показана на рис. 2. Расположенная перед линзой сетка освещается параллельным пучком когерентного света. В задней фокальной плоскости линзы формируется двумерный Фурье-образ сетки — регулярно расположенные по вертикали и по горизонтали световые пятна. Устанавливая в фокальной плоскости различные экраны (фильтрующие маски), можно, закрывая ряд пространственных частот, изменять изображение сетки.
| Фокальная плоскость
плоскость
| | Рис. 2. Схема эксперимента Аббе-Портера
|
Рассмотрим эту процедуру подробнее. Функция пропускания T(x) одномерной сетки размером D c шагом ячейки d и диаметром проволочки l имеет вид, представленный на рис. 3, и описывается формулой
  , ,
где N — число штрихов, 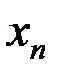 = = 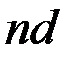 — координата левой границы n-го штриха, — координата левой границы n-го штриха, 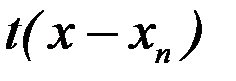 — функция пропускания — функция пропускания 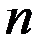 -го штриха: -го штриха:
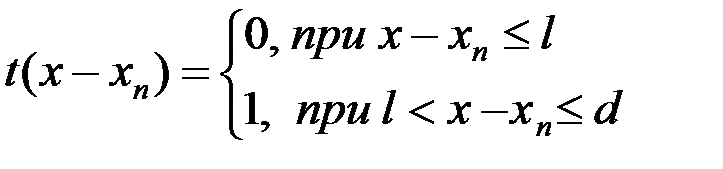 . .
Из рис. 3 видно, что функция пропускания решётки характеризуется тремя пространственными масштабами: шириной штриха  , периодом , периодом 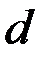 и полным размером и полным размером 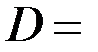 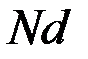 . При интегрировании функции пропускания . При интегрировании функции пропускания 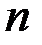 -ого штриха можно заметить, что фаза плоской волны -ого штриха можно заметить, что фаза плоской волны 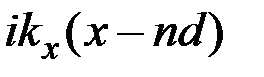 состоит из двух слагаемых: первое меняется непрерывно на ширине штриха, второе — дискретно с шагом состоит из двух слагаемых: первое меняется непрерывно на ширине штриха, второе — дискретно с шагом  при переходе от одного штриха к другому. при переходе от одного штриха к другому.
В соответствии с этим, распределение амплитуды светового поля дифракционной картины в дальней зоне имеет вид произведения двух функций:
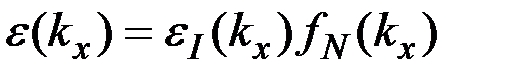 , ,
где первый множитель описывает дифракцию на отдельном штрихе и аналогичен выражению, полученному в предыдущем пункте:
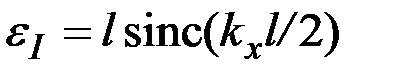 . .
Второй множитель возникает вследствие суммирования (интерференции) волн, испускаемых штрихами как точечными источниками с координатами 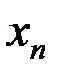 , и вычисляется как сумма , и вычисляется как сумма 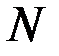 членов геометрической прогрессии: членов геометрической прогрессии:
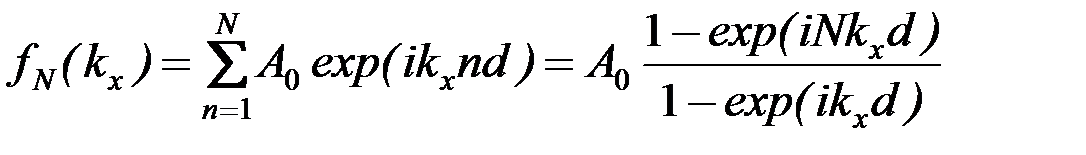 . .
Учитывая, что 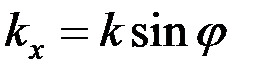 и переходя к интенсивностям светового поля, согласно формуле: и переходя к интенсивностям светового поля, согласно формуле:
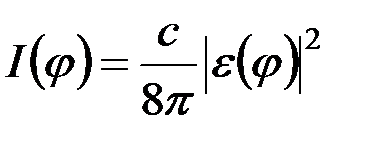 , ,
получим
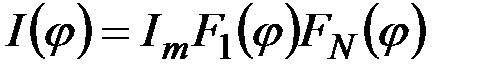 . (11) . (11)
Здесь введены обозначения:
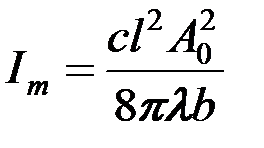 , ,
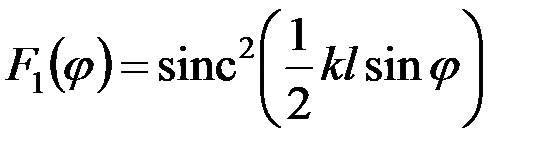 , (12) , (12)
| Рис. 3. Функция пропускания одномерной дифракционной решетки
|
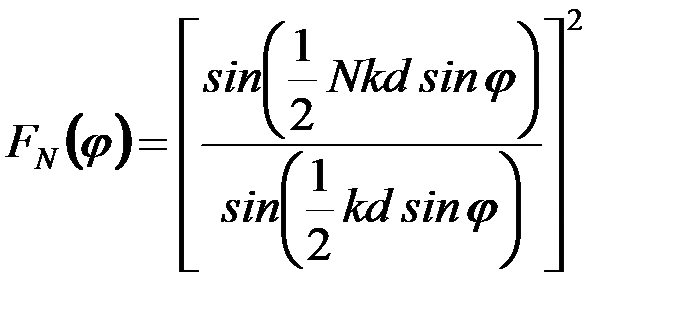 . (13) . (13)
 | Рис. 4. Картина дифракции на одномерной решётке
|
Вид функций  показан на рис. 4. Из рисунка следует, что в структуре дифракционной картины наблюдаются три характерных угловых масштаба: показан на рис. 4. Из рисунка следует, что в структуре дифракционной картины наблюдаются три характерных угловых масштаба:
1) Расстояние между соседними главными максимумами 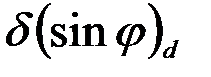 . Оно находится из условия, что распространяющиеся в направлении главных максимумов . Оно находится из условия, что распространяющиеся в направлении главных максимумов 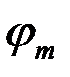 волны, которые излучаются точками решётки, разнесёнными на период волны, которые излучаются точками решётки, разнесёнными на период 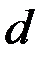 , усиливают друг друга, т. е. их разность фаз кратна , усиливают друг друга, т. е. их разность фаз кратна 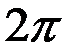 : : 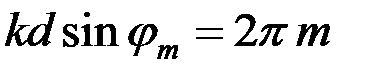 , или , или 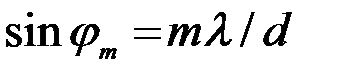 , и , и 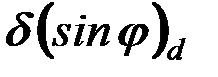 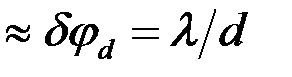 . Здесь . Здесь 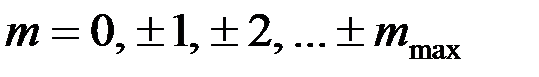 , а максимальный порядок дифракции , а максимальный порядок дифракции 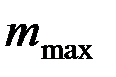 определяется неравенством определяется неравенством 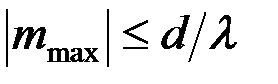 . Из формулы (13) видно, что для этих направлений . Из формулы (13) видно, что для этих направлений 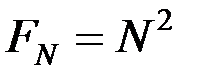 , т. е. интенсивность суммарного светового поля в главных максимумах действительно возрастает в , т. е. интенсивность суммарного светового поля в главных максимумах действительно возрастает в 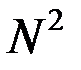 раз, по сравнению с полем одного штриха. раз, по сравнению с полем одного штриха.
2) Ширина главных максимумов  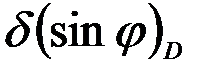 , которая для , которая для  -ого максимума находится из условия, что под углом -ого максимума находится из условия, что под углом 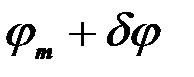 наблюдается ближайший минимум, т. е. согласно формуле (13): наблюдается ближайший минимум, т. е. согласно формуле (13): 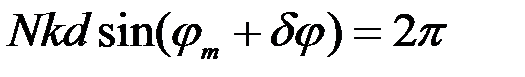 , или , или  = = 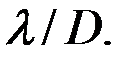
3) Ширина всей картины 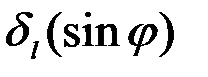 , определяемая характерной шириной функции , определяемая характерной шириной функции 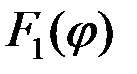 , т. е. условием , т. е. условием 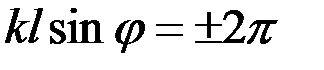 . Отсюда . Отсюда 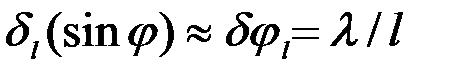 . .
Этим трём масштабам ( 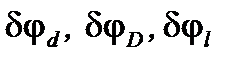 ) в дифракционной картине, представляющей собой Фурье-спектр функции пропускания по переменной ) в дифракционной картине, представляющей собой Фурье-спектр функции пропускания по переменной 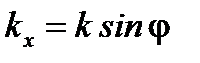 , соответствуют три пространственных масштаба в самой функции , соответствуют три пространственных масштаба в самой функции 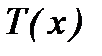 : : 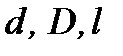 , причём, как видно из формул для , причём, как видно из формул для 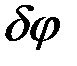 , в соответствии с общими свойствами Фурье-преобразования, каждый масштаб в объекте обратно пропорционален соответствующему масштабу в его спектре. , в соответствии с общими свойствами Фурье-преобразования, каждый масштаб в объекте обратно пропорционален соответствующему масштабу в его спектре.
|

 . Полагая, что амплитуда поля волны, падающей на объект, равна единице, на выходе получим распределение поля вида
. Полагая, что амплитуда поля волны, падающей на объект, равна единице, на выходе получим распределение поля вида 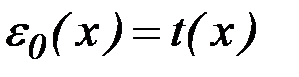 . На расстоянии
. На расстоянии 
 от объекта расположим линзу и построим изображение объекта на произвольном расстоянии
от объекта расположим линзу и построим изображение объекта на произвольном расстоянии 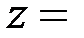
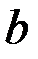 от линзы (рис. 1).
от линзы (рис. 1).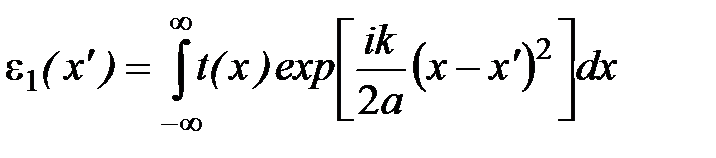 . (3)
. (3)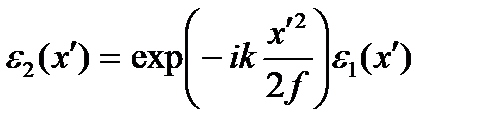 . (4)
. (4)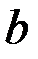 справа от линзы, также описывается соответствующим интегралом Френеля:
справа от линзы, также описывается соответствующим интегралом Френеля: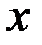 , с помощью линзы, помещённой в плоскости
, с помощью линзы, помещённой в плоскости 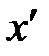 . Справа от линзы на расстоянии
. Справа от линзы на расстоянии 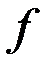 находится фокальная плоскость, на расстоянии
находится фокальная плоскость, на расстоянии 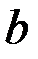 — плоскость изображения
— плоскость изображения
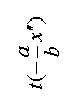

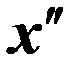
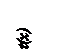
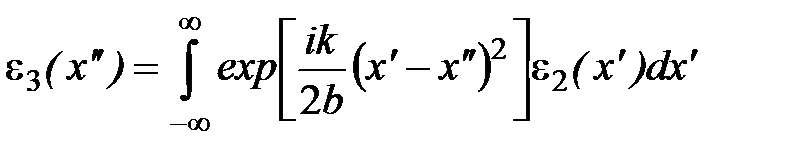 . (5)
. (5)
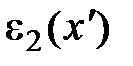 и
и 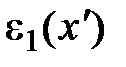 , находим после преобразований
, находим после преобразований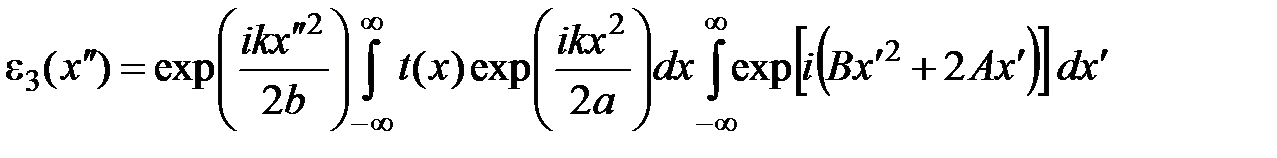 , (6)
, (6)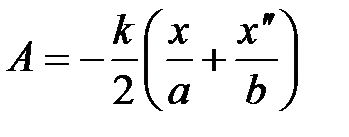 ,
, 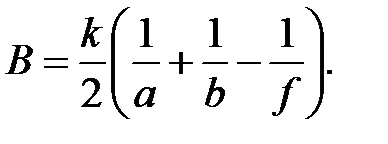 . Последний интеграл в (6) с учётом формулы
. Последний интеграл в (6) с учётом формулы
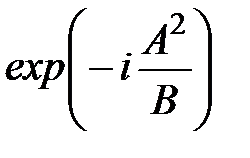
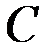 .
.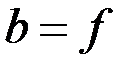 , т.е.
, т.е. 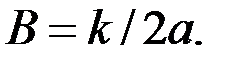 Формула (6) здесь примет вид:
Формула (6) здесь примет вид:
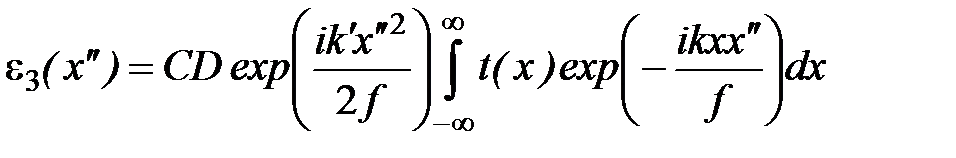 ,
,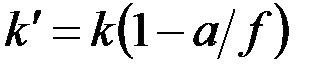 . Отсюда следует, что (с точностью до фазового множителя, не влияющего на распределение интенсивности) в фокальной плоскости линзы формируется Фурье-образ функции пропускания объекта
. Отсюда следует, что (с точностью до фазового множителя, не влияющего на распределение интенсивности) в фокальной плоскости линзы формируется Фурье-образ функции пропускания объекта 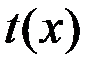 по переменной
по переменной 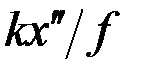 , которая в обычном приближении малых углов дифракции равна поперечной компоненте волнового вектора
, которая в обычном приближении малых углов дифракции равна поперечной компоненте волнового вектора 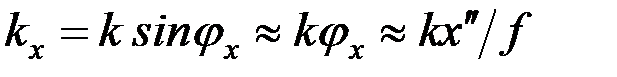 :
: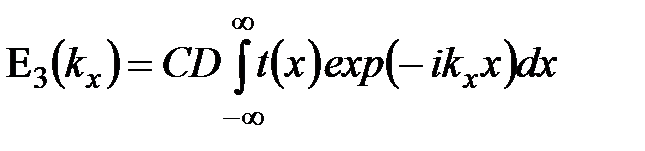 , (7)
, (7)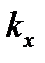 играет роль пространственной частоты.
играет роль пространственной частоты.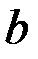 удовлетворяет соотношению:
удовлетворяет соотношению: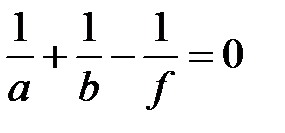 , т.е.
, т.е. 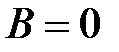 .
.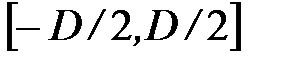 :
: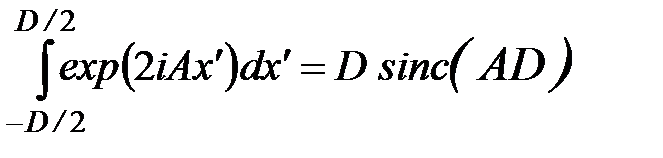 . (8)
. (8)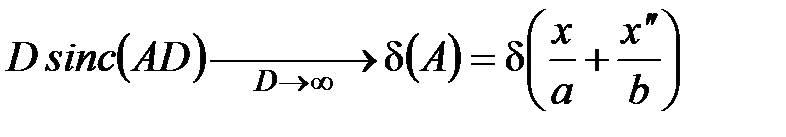 , (9)
, (9)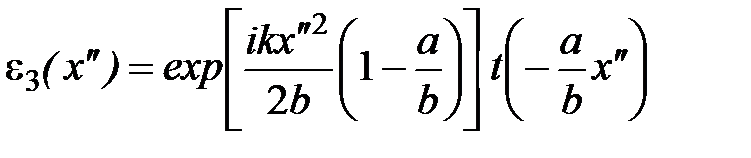 . (10)
. (10) . Поэтому рассматриваемую плоскость естественно назвать плоскостью изображения объекта («перевёрнутого» вследствие знака «минус» в аргументе функции t), масштаб которого, как видно из (10), увеличился в
. Поэтому рассматриваемую плоскость естественно назвать плоскостью изображения объекта («перевёрнутого» вследствие знака «минус» в аргументе функции t), масштаб которого, как видно из (10), увеличился в 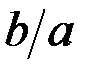 раз. Описанную процедуру построения изображения объекта в виде дифракционной решётки иллюстрирует рис. 1.
раз. Описанную процедуру построения изображения объекта в виде дифракционной решётки иллюстрирует рис. 1. 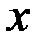 в плоскости объекта переводится линзой в точку с координатой
в плоскости объекта переводится линзой в точку с координатой 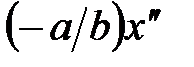 в плоскости изображения только в случае линзы «бесконечно большой», по сравнению с длиной волны. Если же учитывать конечную апертуру линзы, то вместо точки мы получим в плоскости изображение распределения амплитуды светового поля, описываемое функцией
в плоскости изображения только в случае линзы «бесконечно большой», по сравнению с длиной волны. Если же учитывать конечную апертуру линзы, то вместо точки мы получим в плоскости изображение распределения амплитуды светового поля, описываемое функцией  , точнее, с учётом круговой формы апертуры, аналогичной формулой, куда вместо функции sin входит специальная функция — функция Бесселя первого порядка от радиальной координаты. При этом структура светового поля вполне аналогична описываемой функцией
, точнее, с учётом круговой формы апертуры, аналогичной формулой, куда вместо функции sin входит специальная функция — функция Бесселя первого порядка от радиальной координаты. При этом структура светового поля вполне аналогична описываемой функцией  . Характерный угловой размер получившегося центрального светового пятна определяется формулой
. Характерный угловой размер получившегося центрального светового пятна определяется формулой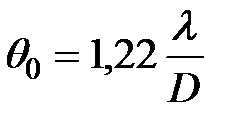

 ,
,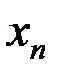 =
= 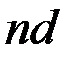 — координата левой границы n-го штриха,
— координата левой границы n-го штриха, 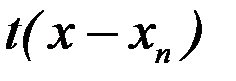 — функция пропускания
— функция пропускания 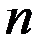 -го штриха:
-го штриха: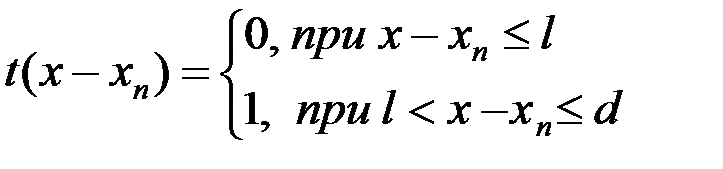 .
. , периодом
, периодом 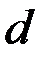 и полным размером
и полным размером 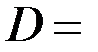
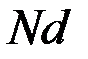 . При интегрировании функции пропускания
. При интегрировании функции пропускания 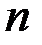 -ого штриха можно заметить, что фаза плоской волны
-ого штриха можно заметить, что фаза плоской волны 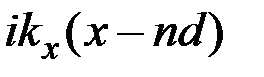 состоит из двух слагаемых: первое меняется непрерывно на ширине штриха, второе — дискретно с шагом
состоит из двух слагаемых: первое меняется непрерывно на ширине штриха, второе — дискретно с шагом  при переходе от одного штриха к другому.
при переходе от одного штриха к другому.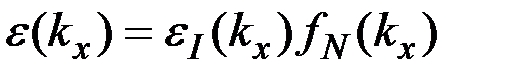 ,
,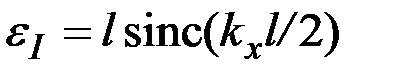 .
.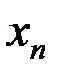 , и вычисляется как сумма
, и вычисляется как сумма 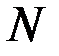 членов геометрической прогрессии:
членов геометрической прогрессии: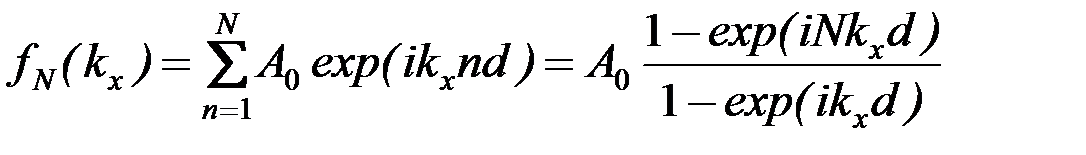 .
.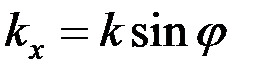 и переходя к интенсивностям светового поля, согласно формуле:
и переходя к интенсивностям светового поля, согласно формуле: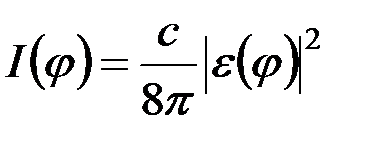 ,
,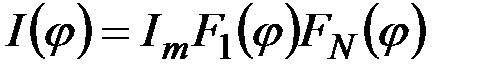 . (11)
. (11)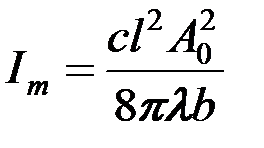 ,
,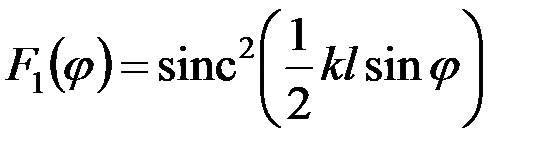 , (12)
, (12)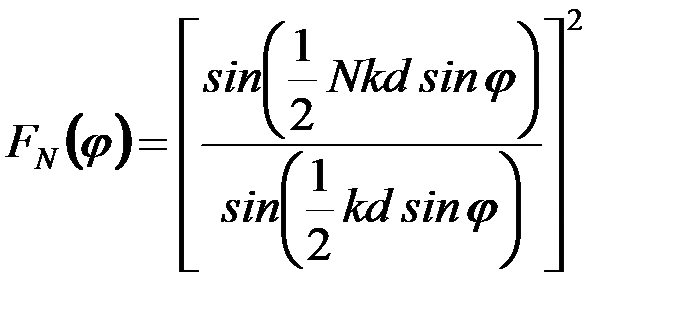 . (13)
. (13)


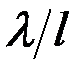
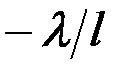

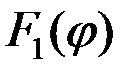



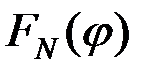

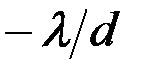

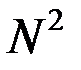

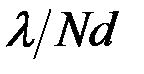



 показан на рис. 4. Из рисунка следует, что в структуре дифракционной картины наблюдаются три характерных угловых масштаба:
показан на рис. 4. Из рисунка следует, что в структуре дифракционной картины наблюдаются три характерных угловых масштаба:
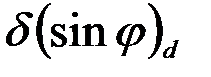 . Оно находится из условия, что распространяющиеся в направлении главных максимумов
. Оно находится из условия, что распространяющиеся в направлении главных максимумов 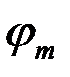 волны, которые излучаются точками решётки, разнесёнными на период
волны, которые излучаются точками решётки, разнесёнными на период 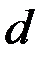 , усиливают друг друга, т. е. их разность фаз кратна
, усиливают друг друга, т. е. их разность фаз кратна 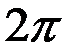 :
: 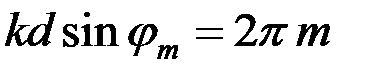 , или
, или 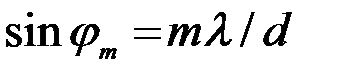 , и
, и 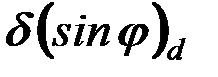
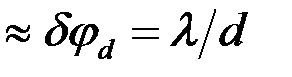 . Здесь
. Здесь 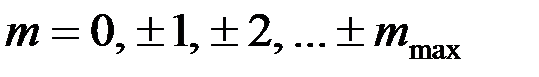 , а максимальный порядок дифракции
, а максимальный порядок дифракции 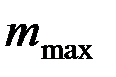 определяется неравенством
определяется неравенством 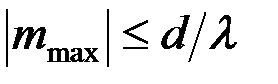 . Из формулы (13) видно, что для этих направлений
. Из формулы (13) видно, что для этих направлений 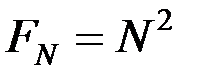 , т. е. интенсивность суммарного светового поля в главных максимумах действительно возрастает в
, т. е. интенсивность суммарного светового поля в главных максимумах действительно возрастает в 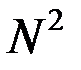 раз, по сравнению с полем одного штриха.
раз, по сравнению с полем одного штриха.
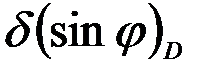 , которая для
, которая для  -ого максимума находится из условия, что под углом
-ого максимума находится из условия, что под углом 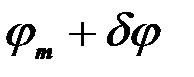 наблюдается ближайший минимум, т. е. согласно формуле (13):
наблюдается ближайший минимум, т. е. согласно формуле (13): 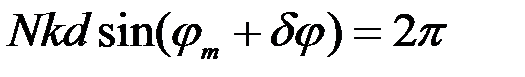 , или
, или  =
= 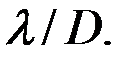
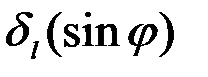 , определяемая характерной шириной функции
, определяемая характерной шириной функции 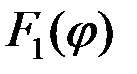 , т. е. условием
, т. е. условием 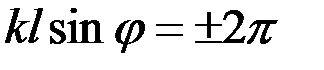 . Отсюда
. Отсюда 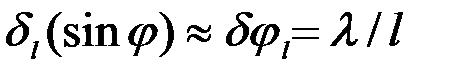 .
.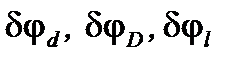 ) в дифракционной картине, представляющей собой Фурье-спектр функции пропускания по переменной
) в дифракционной картине, представляющей собой Фурье-спектр функции пропускания по переменной 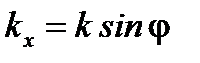 , соответствуют три пространственных масштаба в самой функции
, соответствуют три пространственных масштаба в самой функции 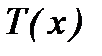 :
: 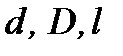 , причём, как видно из формул для
, причём, как видно из формул для 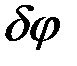 , в соответствии с общими свойствами Фурье-преобразования, каждый масштаб в объекте обратно пропорционален соответствующему масштабу в его спектре.
, в соответствии с общими свойствами Фурье-преобразования, каждый масштаб в объекте обратно пропорционален соответствующему масштабу в его спектре.