
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Контрольная работа по высшей математике №1
Контрольная работа по высшей математике №1
Вариант 1
Задание 1
Вычислить значение функции 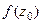 , если
, если
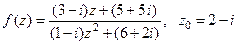 .
.
Изобразить результат на комплексной плоскости и представить его в тригонометрической форме.
Задание 2
Найти 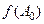 , если
, если 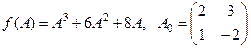 .
.
Задание 3
Найти решение системы линейных алгебраических уравнений
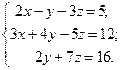
по формулам Крамера.
Задание 4
Найти решение системы линейных алгебраических уравнений
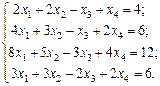
методом Гаусса.
Задание 5
Дано: 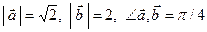 . Для векторов
. Для векторов 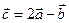 и
и 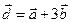 найти скалярное произведение и модуль векторного произведения.
найти скалярное произведение и модуль векторного произведения.
Задание 6
Дан тетраэдр с вершинами в точках
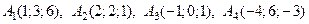 .
.
Найти: 1) внутренние углы в основании 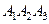 (с точностью до десятых долей градуса), сделать проверку;
(с точностью до десятых долей градуса), сделать проверку;
2) объём пирамиды, площадь основания 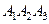 и длину высоты, проведённой из вершины
и длину высоты, проведённой из вершины 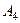 .
.
Задание 7
Прямая 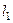 проходит через точки
проходит через точки 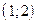 и
и 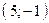 , прямая
, прямая 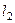 проходит через точки
проходит через точки 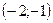 и
и 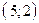 . Составив уравнения прямых, найти точку их пересечения. Для проверки результата сделать чертёж.
. Составив уравнения прямых, найти точку их пересечения. Для проверки результата сделать чертёж.
Задание 8
Найти точку пересечения прямой 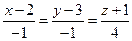 и плоскости
и плоскости 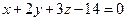 . Отметить найденную точку в трёхмерной декартовой системе координат.
. Отметить найденную точку в трёхмерной декартовой системе координат.
Вариант 2
Задание 1
Вычислить значение функции 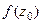 , если
, если
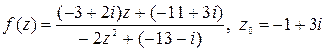 .
.
Изобразить результат на комплексной плоскости и представить его в тригонометрической форме.
Задание 2
Найти 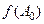 , если
, если 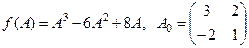 .
.
Задание 3
Найти решение системы линейных алгебраических уравнений
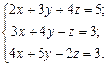
по формулам Крамера.
Задание 4
Найти решение системы линейных алгебраических уравнений
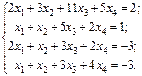
методом Гаусса.
Задание 5
Дано: 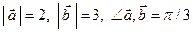 . Для векторов
. Для векторов 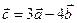 и
и 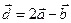 найти скалярное произведение и модуль векторного произведения.
найти скалярное произведение и модуль векторного произведения.
Задание 6
Дан тетраэдр с вершинами в точках
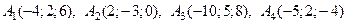 .
.
Найти: 1) внутренние углы в основании 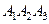 (с точностью до десятых долей градуса), сделать проверку;
(с точностью до десятых долей градуса), сделать проверку;
2) объём пирамиды, площадь основания 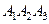 и длину высоты, проведённой из вершины
и длину высоты, проведённой из вершины 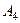 .
.
Задание 7
Прямая 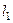 проходит через точки
проходит через точки 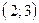 и
и 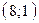 , прямая
, прямая 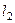 проходит через точки
проходит через точки 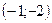 и
и 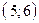 . Составив уравнения прямых, найти точку их пересечения. Для проверки результата сделать чертёж.
. Составив уравнения прямых, найти точку их пересечения. Для проверки результата сделать чертёж.
Задание 8
Найти точку пересечения прямой 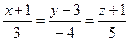 и плоскости
и плоскости 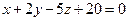 . Отметить найденную точку в трёхмерной декартовой системе координат.
. Отметить найденную точку в трёхмерной декартовой системе координат.
Вариант 3
Задание 1
Вычислить значение функции 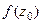 , если
, если
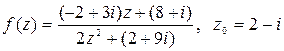 .
.
Изобразить результат на комплексной плоскости и представить его в тригонометрической форме.
Задание 2
Найти 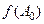 , если
, если 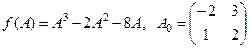 .
.
Задание 3
Найти решение системы линейных алгебраических уравнений
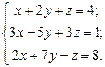
по формулам Крамера.
Задание 4
Найти решение системы линейных алгебраических уравнений
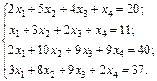
методом Гаусса.
Задание 5
Дано: 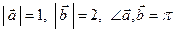 . Для векторов
. Для векторов 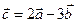 и
и 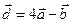 найти скалярное произведение и модуль векторного произведения.
найти скалярное произведение и модуль векторного произведения.
Задание 6
Дан тетраэдр с вершинами в точках
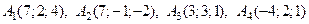 .
.
Найти: 1) внутренние углы в основании 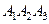 (с точностью до десятых долей градуса), сделать проверку;
(с точностью до десятых долей градуса), сделать проверку;
2) объём пирамиды, площадь основания 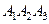 и длину высоты, проведённой из вершины
и длину высоты, проведённой из вершины 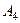 .
.
Задание 7
Прямая 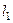 проходит через точки
проходит через точки 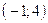 и
и 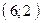 , прямая
, прямая 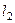 проходит через точки
проходит через точки 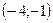 и
и 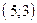 . Составив уравнения прямых, найти точку их пересечения. Для проверки результата сделать чертёж.
. Составив уравнения прямых, найти точку их пересечения. Для проверки результата сделать чертёж.
Задание 8
Найти точку пересечения прямой 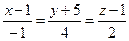 и плоскости
и плоскости 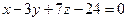 . Отметить найденную точку в трёхмерной декартовой системе координат.
. Отметить найденную точку в трёхмерной декартовой системе координат.
Вариант 4
Задание 1
Вычислить значение функции 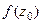 , если
, если
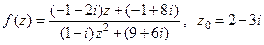 .
.
Изобразить результат на комплексной плоскости и представить его в тригонометрической форме.
Задание 2
Найти 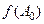 , если
, если 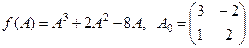 .
.
Задание 3
Найти решение системы линейных алгебраических уравнений
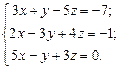
по формулам Крамера.
Задание 4
Найти решение системы линейных алгебраических уравнений
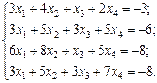
методом Гаусса.
Задание 5
Дано:  . Для векторов
. Для векторов 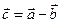 и
и 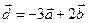 найти скалярное произведение и модуль векторного произведения.
найти скалярное произведение и модуль векторного произведения.
Задание 6
Дан тетраэдр с вершинами в точках
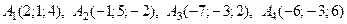 .
.
Найти: 1) внутренние углы в основании 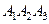 (с точностью до десятых долей градуса), сделать проверку;
(с точностью до десятых долей градуса), сделать проверку;
2) объём пирамиды, площадь основания 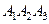 и длину высоты, проведённой из вершины
и длину высоты, проведённой из вершины 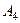 .
.
Задание 7
Прямая 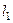 проходит через точки
проходит через точки 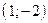 и
и 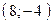 , прямая
, прямая 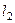 проходит через точки
проходит через точки 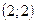 и
и 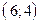 . Составив уравнения прямых, найти точку их пересечения. Для проверки результата сделать чертёж.
. Составив уравнения прямых, найти точку их пересечения. Для проверки результата сделать чертёж.
Задание 8
Найти точку пересечения прямой 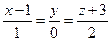 и плоскости
и плоскости  . Отметить найденную точку в трёхмерной декартовой системе координат.
. Отметить найденную точку в трёхмерной декартовой системе координат.
Вариант 5
Задание 1
Вычислить значение функции 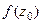 , если
, если
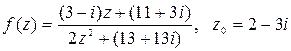 .
.
Изобразить результат на комплексной плоскости и представить его в тригонометрической форме.
Задание 2
Найти 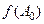 , если
, если 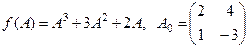 .
.
Задание 3
Найти решение системы линейных алгебраических уравнений
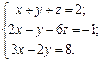
по формулам Крамера.
Задание 4
Найти решение системы линейных алгебраических уравнений
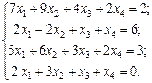
методом Гаусса.
Задание 5
Дано: 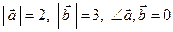 . Для векторов
. Для векторов 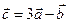 и
и 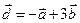 найти скалярное произведение и модуль векторного произведения.
найти скалярное произведение и модуль векторного произведения.
Задание 6
Дан тетраэдр с вершинами в точках
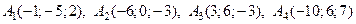 .
.
Найти: 1) внутренние углы в основании 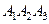 (с точностью до десятых долей градуса), сделать проверку;
(с точностью до десятых долей градуса), сделать проверку;
2) объём пирамиды, площадь основания 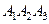 и длину высоты, проведённой из вершины
и длину высоты, проведённой из вершины 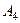 .
.
Задание 7
Прямая 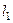 проходит через точки
проходит через точки 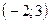 и
и 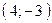 , прямая
, прямая 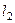 проходит через точки
проходит через точки 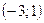 и
и 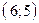 . Составив уравнения прямых, найти точку их пересечения. Для проверки результата сделать чертёж.
. Составив уравнения прямых, найти точку их пересечения. Для проверки результата сделать чертёж.
Задание 8
Найти точку пересечения прямой  и плоскости
и плоскости 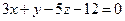 . Отметить найденную точку в трёхмерной декартовой системе координат.
. Отметить найденную точку в трёхмерной декартовой системе координат.
Вариант 6
Задание 1
Вычислить значение функции 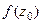 , если
, если
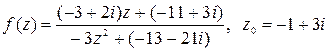 .
.
Изобразить результат на комплексной плоскости и представить его в тригонометрической форме.
Задание 2
Найти 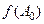 , если
, если  .
.
Задание 3
Найти решение системы линейных алгебраических уравнений
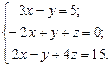
по формулам Крамера.
Задание 4
Найти решение системы линейных алгебраических уравнений
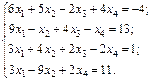
методом Гаусса.
Задание 5
Дано: 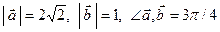 . Для векторов
. Для векторов 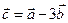 и
и 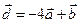 найти скалярное произведение и модуль векторного произведения.
найти скалярное произведение и модуль векторного произведения.
Задание 6
Дан тетраэдр с вершинами в точках
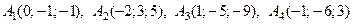 .
.
Найти: 1) внутренние углы в основании 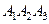 (с точностью до десятых долей градуса), сделать проверку;
(с точностью до десятых долей градуса), сделать проверку;
2) объём пирамиды, площадь основания 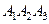 и длину высоты, проведённой из вершины
и длину высоты, проведённой из вершины 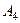 .
.
Задание 7
Прямая 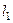 проходит через точки
проходит через точки 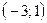 и
и 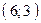 , прямая
, прямая 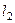 проходит через точки
проходит через точки 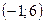 и
и 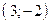 . Составив уравнения прямых, найти точку их пересечения. Для проверки результата сделать чертёж.
. Составив уравнения прямых, найти точку их пересечения. Для проверки результата сделать чертёж.
Задание 8
Найти точку пересечения прямой 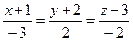 и плоскости
и плоскости 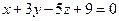 . Отметить найденную точку в трёхмерной декартовой системе координат.
. Отметить найденную точку в трёхмерной декартовой системе координат.
Вариант 7
Задание 1
Вычислить значение функции 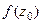 , если
, если
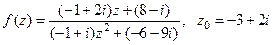 .
.
Изобразить результат на комплексной плоскости и представить его в тригонометрической форме.
Задание 2
Найти 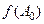 , если
, если 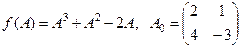 .
.
Задание 3
Найти решение системы линейных алгебраических уравнений
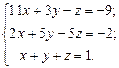
по формулам Крамера.
Задание 4
Найти решение системы линейных алгебраических уравнений
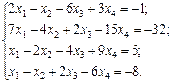
методом Гаусса.
Задание 5
Дано: 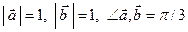 . Для векторов
. Для векторов 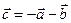 и
и 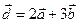 найти скалярное произведение и модуль векторного произведения.
найти скалярное произведение и модуль векторного произведения.
Задание 6
Дан тетраэдр с вершинами в точках
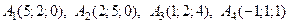 .
.
Найти: 1) внутренние углы в основании 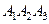 (с точностью до десятых долей градуса), сделать проверку;
(с точностью до десятых долей градуса), сделать проверку;
2) объём пирамиды, площадь основания 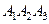 и длину высоты, проведённой из вершины
и длину высоты, проведённой из вершины 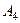 .
.
Задание 7
Прямая 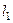 проходит через точки
проходит через точки 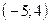 и
и  , прямая
, прямая 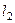 проходит через точки
проходит через точки 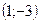 и
и 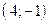 . Составив уравнения прямых, найти точку их пересечения. Для проверки результата сделать чертёж.
. Составив уравнения прямых, найти точку их пересечения. Для проверки результата сделать чертёж.
Задание 8
Найти точку пересечения прямой 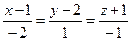 и плоскости
и плоскости 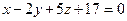 . Отметить найденную точку в трёхмерной декартовой системе координат.
. Отметить найденную точку в трёхмерной декартовой системе координат.
Вариант 8
Задание 1
Вычислить значение функции 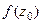 , если
, если
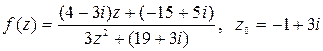 .
.
Изобразить результат на комплексной плоскости и представить его в тригонометрической форме.
Задание 2
Найти 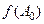 , если
, если 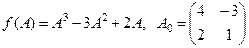 .
.
Задание 3
Найти решение системы линейных алгебраических уравнений
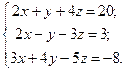
по формулам Крамера.
Задание 4
Найти решение системы линейных алгебраических уравнений
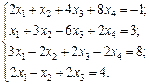
методом Гаусса.
Задание 5
Дано: 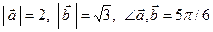 . Для векторов
. Для векторов 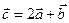 и
и 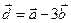 найти скалярное произведение и модуль векторного произведения.
найти скалярное произведение и модуль векторного произведения.
Задание 6
Дан тетраэдр с вершинами в точках
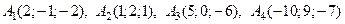 .
.
Найти: 1) внутренние углы в основании 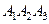 (с точностью до десятых долей градуса), сделать проверку;
(с точностью до десятых долей градуса), сделать проверку;
2) объём пирамиды, площадь основания 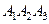 и длину высоты, проведённой из вершины
и длину высоты, проведённой из вершины 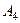 .
.
Задание 7
Прямая 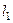 проходит через точки
проходит через точки  и
и 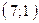 , прямая
, прямая 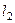 проходит через точки
проходит через точки 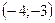 и
и 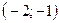 . Составив уравнения прямых, найти точку их пересечения. Для проверки результата сделать чертёж.
. Составив уравнения прямых, найти точку их пересечения. Для проверки результата сделать чертёж.
Задание 8
Найти точку пересечения прямой 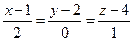 и плоскости
и плоскости 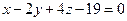 . Отметить найденную точку в трёхмерной декартовой системе координат.
. Отметить найденную точку в трёхмерной декартовой системе координат.
Вариант 9
Задание 1
Вычислить значение функции 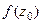 , если
, если
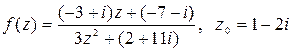 .
.
Изобразить результат на комплексной плоскости и представить его в тригонометрической форме.
Задание 2
Найти 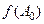 , если
, если 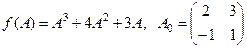 .
.
Задание 3
Найти решение системы линейных алгебраических уравнений
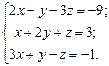
по формулам Крамера.
Задание 4
Найти решение системы линейных алгебраических уравнений
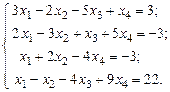
методом Гаусса.
Задание 5
Дано: 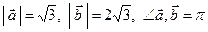 . Для векторов
. Для векторов 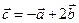 и
и  найти скалярное произведение и модуль векторного произведения.
найти скалярное произведение и модуль векторного произведения.
Задание 6
Дан тетраэдр с вершинами в точках
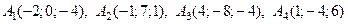 .
.
Найти: 1) внутренние углы в основании 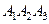 (с точностью до десятых долей градуса), сделать проверку;
(с точностью до десятых долей градуса), сделать проверку;
2) объём пирамиды, площадь основания 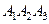 и длину высоты, проведённой из вершины
и длину высоты, проведённой из вершины 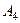 .
.
Задание 7
Прямая 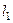 проходит через точки
проходит через точки 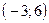 и
и 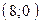 , прямая
, прямая 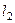 проходит через точки
проходит через точки 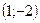 и
и 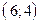 . Составив уравнения прямых, найти точку их пересечения. Для проверки результата сделать чертёж.
. Составив уравнения прямых, найти точку их пересечения. Для проверки результата сделать чертёж.
Задание 8
Найти точку пересечения прямой 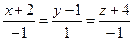 и плоскости
и плоскости 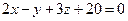 . Отметить найденную точку в трёхмерной декартовой системе координат.
. Отметить найденную точку в трёхмерной декартовой системе координат.
Вариант 10
Задание 1
Вычислить значение функции 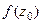 , если
, если
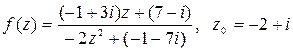 .
.
Изобразить результат на комплексной плоскости и представить его в тригонометрической форме.
Задание 2
Найти 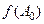 , если
, если 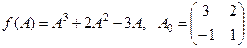 .
.
Задание 3
Найти решение системы линейных алгебраических уравнений

по формулам Крамера.
Задание 4
Найти решение системы линейных алгебраических уравнений
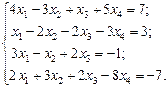
методом Гаусса.
Задание 5
Дано: 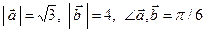 . Для векторов
. Для векторов 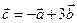 и
и 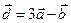 найти скалярное произведение и модуль векторного произведения.
найти скалярное произведение и модуль векторного произведения.
Задание 6
Дан тетраэдр с вершинами в точках
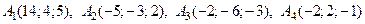 .
.
Найти: 1) внутренние углы в основании 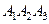 (с точностью до десятых долей градуса), сделать проверку;
(с точностью до десятых долей градуса), сделать проверку;
2) объём пирамиды, площадь основания 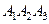 и длину высоты, проведённой из вершины
и длину высоты, проведённой из вершины 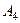 .
.
Задание 7
Прямая 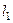 проходит через точки
проходит через точки 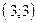 и
и 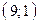 , прямая
, прямая 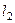 проходит через точки
проходит через точки 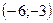 и
и 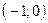 . Составив уравнения прямых, найти точку их пересечения. Для проверки результата сделать чертёж.
. Составив уравнения прямых, найти точку их пересечения. Для проверки результата сделать чертёж.
Задание 8
Найти точку пересечения прямой 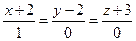 и плоскости
и плоскости 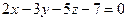 . Отметить найденную точку в трёхмерной декартовой системе координат.
. Отметить найденную точку в трёхмерной декартовой системе координат.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|