Тема № 4 . ИНФОРМАЦИОННЫЕ ПРОЦЕССЫ

Стр 1 из 3Следующая ⇒

Учебная дисциплина: ОДП.04. Информатика и ИКТ.

Группа: АМ-2-19.

Профессия: 23.01.03.Автомеханик

Дата проведения: 10.06.20 г.

Тема № 4 . ИНФОРМАЦИОННЫЕ ПРОЦЕССЫ

Урок № 38

Тема: ПРОГРАММИРОВАНИЕ МОДЕЛИ РАБОТЫ АЛГОРИТМА ХЕММИНГА.

Цель урока: обобщить знания по программированию алгоритма Хемминга.

На предыдущем уроке мы рассмотрели код Хемминга, изучили алгоритм построения кода Хемминга, а также удостоверились, что код Хемминга ищет и исправляет одиночную и двойную ошибку.

Сегодня мы рассмотрим еще несколько примеров практического применения кода Хемминга.

На предыдущем уроке было выдано задание: Построить код Хемминга для передачи сообщений в виде последовательности десятичных цифр, представленных в виде 4 –х разрядных двоичных слов. Показать процесс кодирования, декодирования и исправления одиночной ошибки на примере информационного слова 0101.

Проверьте свои знания:

Решение примера использования кода Хемминга

для нахождения одной ошибки

1. По заданной длине информационного слова (k = 4), определим количество контрольных разрядов m, используя соотношение:

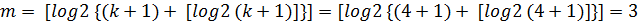при этом 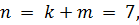т. е. получили (7, 4) -код.

2. Определяем номера рабочих и контрольных позиции кодовой комбинации. Номера контрольных позиций выбираем по закону .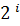

Для рассматриваемой задачи (при n = 7) номера контрольных позиций равны 1, 2, 4. При этом кодовая комбинация имеет вид:

b1 b2 b3 b4 b5 b6 b7

k1 k2 0 k2 1 0 1

3. Определяем значения контрольных разрядов (0 или 1), используя проверочную матрицу.

Первая проверка:

k1b3 b5 b7 = k1 011 будет четной при k1 = 0.

Вторая проверка:

k2 b3 b6 b7 = k2 001 будет четной при k2 = 1.

Третья проверка:

k3 b5 b6 b7 = k3 101 будет четной при k3 = 0.

1 2 3 4 5 6 7

Передаваемая кодовая комбинация: 0100101.

Допустим принято: 0110101.

Для обнаружения и исправления ошибки составим аналогичные проверки на четность контрольных сумм, в соответствии с проверочной матрицей результатом которых является двоичное ( 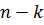) – разрядное число, называемое синдромом и указывающим на положение ошибки, т. е, номер ошибочной позиции.

1) k1= b3 b5 b7 = 0111 = 1.

2) k2=b3 b6 b7 = 1101 = 1.

3) k3 =b5 b6 b7 = 0101 =0.

Сравнивая синдром ошибки со столбцами проверочной матрицы, определяем номер ошибочного бита. Синдрому 011 соответствует третий столбец, т. е. ошибка в третьем разряде кодовой комбинации. Символ в третьей позиции необходимо изменить на обратный.

А сейчас рассмотрим следующее:

12 3 Следующая ⇒