E1- Е2 = -UR1 - UR2 или E1 = Е2 - UR1 - UR2 (3)

E1- Е2 = -UR1 - UR2 или E1 = Е2 - UR1 - UR2 (3)

Предлагаю посмотреть отдельный видеоурок по второму закону Кирхогфа (теория).

Расчеты электрических цепей с помощью законов Кирхгофа.

Теперь давайте рассмотрим вариант сложной цепи, и я вам расскажу, как на практике применять законы Кирхгофа.

Итак, на рисунке 4 имеется сложная цепь с двумя источниками ЭДС величиной E₁=12 в и E₂=5 в , с внутренним сопротивлением источниковr₁=r₂=0,1 Ом, работающих на общую нагрузку R = 2 Ома. Как же будут распределены токи в этой цепи, и какие они имеют значения, нам предстоит выяснить.

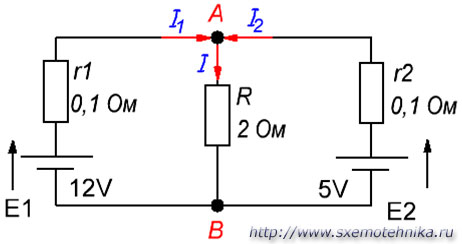
Рисунок 4. Пример расчета сложной электрической цепи.

Теперь согласно первому закону Кирхгофа для узла А составляем такое выражение:

I = I₁ + I₂,

так как I₁ и I₂ втекают в узел А, а ток I вытекает из него.

Используя второй закон Кирхгофа, запишем еще два выражения для внешнего контура и внутреннего левого контура, выбрав направление обхода по часовой стрелке.

Для внешнего контура:

E₁-E₂ = Ur₁ – Ur₂ или E₁-E₂ = I₁*r₁ – I₂*r₂

Для внутреннего левого контура:

E1 = Ur1 + UR или E1 = I1*r1 + I*R

Итак, у нас получилась система их трех уравнений с тремя неизвестными:

I = I1 + I2;

E1-E2 = I1*r1 – I2*r2;

E1 = I1*r1 + I*R.

Теперь подставим в эту систему известные нам величины напряжений и сопротивлений:

I = I1 + I2;

7 = 0,1I1 – 0,1I2;

12 = 0,1I1 +2I.

Далее из первого и второго уравнения выразим ток I₂

I2=I - I1;

I2 = I1 – 70;

12 = 0,1I1 + 2I.

Следующим шагом приравняем первое и второе уравнение и получим систему из двух уравнений:

I - I1= I1 – 70;

12 = 0,1I1 + 2I.

Выражаем из первого уравнения значение I

I = 2I1– 70;

И подставляем его значение во второе уравнение

12 = 0,1I1 + 2(2I1 – 70).

Решаем полученное уравнение

12 = 0,1I1 + 4I1 – 140.

12 + 140= 4,1I₁

I1=152/4,1

I1=37,073 (А)

Теперь в выражениеI = 2I₁– 70 подставим значение

I₁=37,073 (А) и получим:

I = 2*37,073 – 70 = 4,146 А

Ну, а согласно первому закона Кирхгофа ток I₂=I - I₁

I2=4,146 - 37,073 = -32,927

Знак «минус» для тока I₂ означает, то что мы не правильно выбрали направление тока, то есть в нашем случае ток I₂ вытекает из узла А.

РАСЧЕТ ЭЛЕКТРИЧЕСКОЙ ЦЕПИ МЕТОДОМ КОНТУРНЫХ ТОКОВ

При расчете цепи методом контурных токов выдвигаются два предположения:

· в каждом контуре протекают независимые друг от друга расчетные (контурные) токи;

· ток каждой ветви равен алгебраической сумме контурных токов, протекающих через эту ветвь.

При расчете рекомендуется следующая последовательность действий:

· находят в цепи ветви, узлы и контуры;

· указывают произвольные направления токов в ветвях и направления обхода контуров;

· произвольно выбирают направления контурных токов, обычно совпадающие с направлениями обхода контура;

· для независимых контуров составляют уравнения по второму закону Кирхгофа относительно неизвестных контурных токов I₁, I₁₁, I₁₁₁.

Для рассчитываемой электрической цепи система уравнений будет иметь вид:

· для контура acef: (R_I + r₀₁ + R₃) I_I – R₃ I_II =E₁

· для контура abc: -R₃ I_I + (R₂ + R₃ +R₄) I_II — R₂ I_III = -E₂

· для контура bdc: -R₃ I_II + (R₂ + R₅ +R₆) I_III = E₂

В рассматриваемом примере при составлении уравнений принято во внимание то, что вторая (R₂, E₂) и третья (R_з) ветви электрической цепи являются смежными и по ним протекают два контурных тока, каждый из которых обусловливает на резисторе смежной ветви падение напряжения, например, R₂I_II и R₂I_III (для токов второй ветви).

r₀₁ – внутреннее сопротивление источника ЭДС Е₁.

Токи в ветвях определяют алгебраическим суммированием контурных токов, протекающих через ту или иную ветвь. Контурный ток берется со знаком «плюс», если его направление совпадает с направлением тока ветви, и со знаком «минус» — при встречном направлении.

⇐ Предыдущая 1 23