
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Политропные процессы
Политропные процессы
Политропными называются ТД процессы, у которых закон распределения энергии характеризуется условием 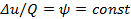 в течение всего процесса. Т.е. основными характеристиками политропного процесса являются уравнения
в течение всего процесса. Т.е. основными характеристиками политропного процесса являются уравнения 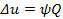 и
и 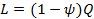 .
.
Все ранее рассмотренные процессы являются политропными, но с явно выраженными внешними признаками в виде 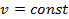 ,
, 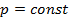 ,
, 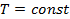 или
или 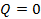 . В общем случае таких признаков может не быть. Политропные процессы подчиняются уравнению
. В общем случае таких признаков может не быть. Политропные процессы подчиняются уравнению 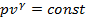 , где
, где 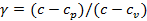 – показатель политропного процесса;
– показатель политропного процесса; 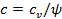 – теплоёмкость политропного процесса. Уравнение политропного процесса
– теплоёмкость политропного процесса. Уравнение политропного процесса 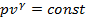 является обобщающим уравнением для всех ТД процессов с постоянным законом распределения энергии, в том числе для ранее рассмотренных.
является обобщающим уравнением для всех ТД процессов с постоянным законом распределения энергии, в том числе для ранее рассмотренных.
Для изохорного процесса уравнение можно представить в виде 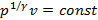 , т.е. что может быть получено только при
, т.е. что может быть получено только при 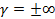 . Для изобарного процесса уравнение
. Для изобарного процесса уравнение 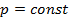 может быть получено из уравнения политропы в случае, если
может быть получено из уравнения политропы в случае, если 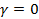 , т.к.
, т.к. 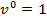 , и, следовательно,
, и, следовательно, 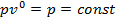 . Для изотермического процесса (
. Для изотермического процесса ( 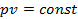 )
) 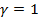 ; для адиабатного (
; для адиабатного ( 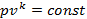 )
) 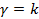 .
.
Способ построения политропных процессов такой же, как и адиабатных.
Формулы соотношения параметров выводятся так же, как для адиабатного процесса, т.е. являются следствием уравнений 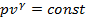 и
и 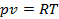 , но показатель
, но показатель 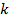 заменён показателем
заменён показателем 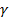 :
:
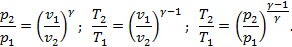
Формулы работы в политропных процессах будут также аналогичны формулам в адиабатном процессе только вместо показателя 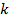 в них будет показатель
в них будет показатель 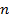 . При этом получим:
. При этом получим:
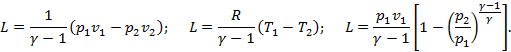
Кроме того, работа в политропном процессе может быть определена по характеристическому уравнению 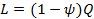 .
.
Формула теплоёмкости политропного процесса
Из формулы 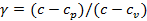 находим
находим 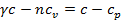 , откуда
, откуда 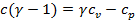 или
или
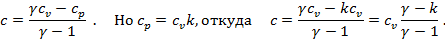
Подставляя в уравнение различные значения 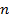 , получим формулы теплоёмкости основных процессов:
, получим формулы теплоёмкости основных процессов:
Изохорный процесс ( 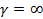 ): Представим полученное уравнение для теплоёмкости в виде
): Представим полученное уравнение для теплоёмкости в виде

Следовательно, 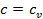 .
.
Изобарный процесс ( 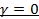 ): Подставляя значение
): Подставляя значение 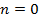 в уравнение, получим
в уравнение, получим
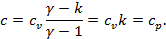
Изотермический процесс ( 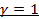 ):
):
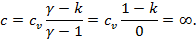
Адиабатный процесс ( 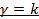 ):
):
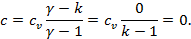
Коэффициент 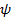 , характеризующий закон распределения энергии в политропных процессах, также можно выразить через показатель политропы
, характеризующий закон распределения энергии в политропных процессах, также можно выразить через показатель политропы 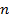 . Из уравнения
. Из уравнения 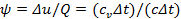 следует, что
следует, что 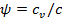 . Подставляя в это уравнение значение
. Подставляя в это уравнение значение 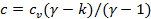 , получим
, получим
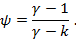
Изменение внутренней энергии в политропных процессах определяется так же, как и во всех процессах по уравнению 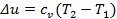 или по характеристическому уравнению
или по характеристическому уравнению
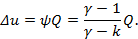
Внешняя теплота, участвующая в политропных процессах, определяется либо по первому закону термодинамики 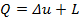 , либо по уравнениям
, либо по уравнениям
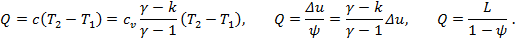
Взаимное расположение изотермы и адиабаты в v-p координатах
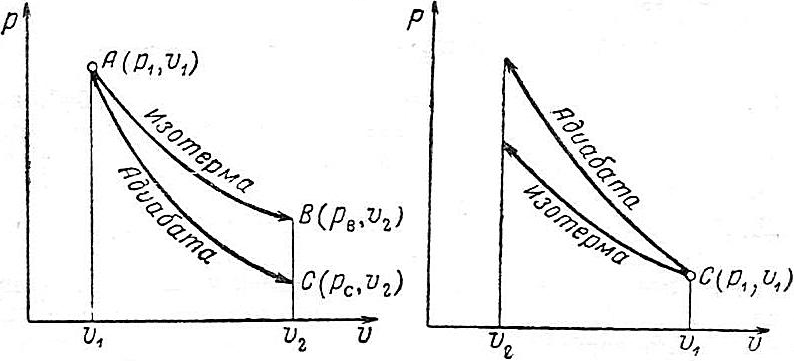
Определение показателя политропы n
Для определения характеристик политропного процесса необходимо знать значение показателя политропы 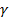 . Если в координатах p-vдана политропа, то по её виду и расположению можно определить показатель политропы
. Если в координатах p-vдана политропа, то по её виду и расположению можно определить показатель политропы 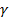 . Если же нанесён произвольный процесс (рис.4.16), то прежде, чем определить
. Если же нанесён произвольный процесс (рис.4.16), то прежде, чем определить 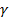 , необходимо проверить, подчиняется ли он закономерностям политропного процесса.
, необходимо проверить, подчиняется ли он закономерностям политропного процесса.
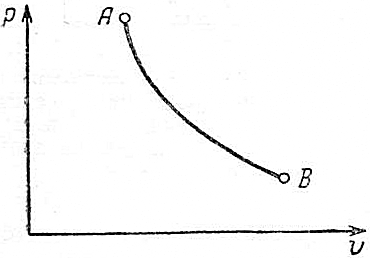 Рис. 4.16.
Рис. 4.16.
| 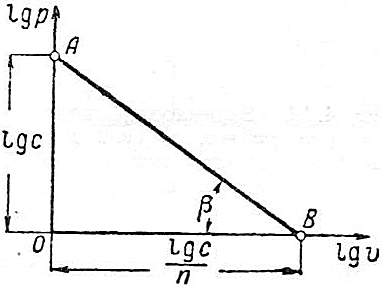 Рис. 4.17.
Рис. 4.17.
|
Для этого воспользуемся тем геометрическим свойством политропного процесса, что изображение его в координатах 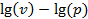 – прямая линия. Логарифмируя уравнение
– прямая линия. Логарифмируя уравнение 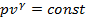 , находим
, находим 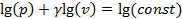 и получаем уравнение прямой в lg-координатах. Для построения этой прямой достаточно знать две точки. Пусть
и получаем уравнение прямой в lg-координатах. Для построения этой прямой достаточно знать две точки. Пусть 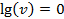 , тогда
, тогда 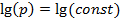 (рис.4.17). А при
(рис.4.17). А при 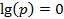 имеем
имеем 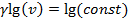 или
или 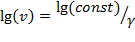 . Видно, что
. Видно, что 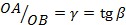 . Т.е. при построении политропного процесса в координатах lg(v)–lg(p)тангенс наклона прямой к оси lg(v) численно равен показателю политропного процесса. В зависимости от константы, определяемой выбором начальной точки, и показателя
. Т.е. при построении политропного процесса в координатах lg(v)–lg(p)тангенс наклона прямой к оси lg(v) численно равен показателю политропного процесса. В зависимости от константы, определяемой выбором начальной точки, и показателя 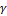 , определяющего характер процесса, прямые lg(p)+γlg(v)=lg(c) изображаются, как показано на рис. 4.17 и 4.18.
, определяющего характер процесса, прямые lg(p)+γlg(v)=lg(c) изображаются, как показано на рис. 4.17 и 4.18.
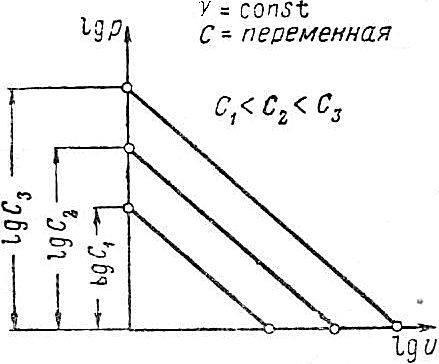 Рис. 4.18.
Рис. 4.18.
| 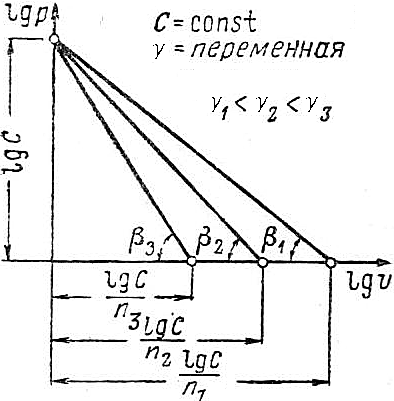 Рис. 4.19.
Рис. 4.19.
|
Пусть теперь задана некая кривая в p-v координатах. Чтобы определить, является ли она политропой, наносим в координатах lg(v)–lg(p) точки A1 и B1 с координатами lg(p1), lg(v1) и lg(p2), lg(v2), т.е. начальную и конечную точки процесса. Проводим через эти точки прямую. Берём в системе p-v любую точку D, лежащую на кривой AB и имеющую координаты v3, p3, и наносим точку D1 с координатами lg(v3) и lg(p3) в логарифмической системе координат. Если эта точка попадает на прямую A1B1, то это указывает на то, что кривая в p-v координатах изображает политропный процесс, если же не попадает, то не является. Подводя итог, можно сделать следующий вывод: если кривая какого-либо процесса, изображённая в p-v координатах, при её изображении в системе lg(v)–lg(p) координат принимает вид прямой, то процесс, изображённый этой кривой, будет политропным.
Показатель политропы можно вычислить, применяя формулы соотношения параметров политропного процесса. Логарифмируя соотношение
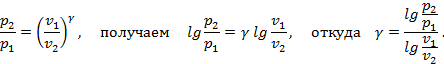
Исследование политропных процессов
Основными задачами исследования являются выявление типичных групп политропных процессов и определение их особенностей и характеристик. Рассмотрим графики основных процессов в координатах v-p (рис.4.22) и выявим типичные особенности политропных процессов по характеру изменения Δu и Q.
| Рассмотрим сначала изменение внутренней энергии в политропных процессах. В изотермическом процессе при T=const (жирная линия на рис.4.22) внутренняя энергия не меняется (Δu=0). Очевидно, что во всех других случаях внутренняя энергия или уменьшается, или увеличивается. Если в области расширения от точки A идти вверх по направлению стрелки, то встречается процесс изобарного расширения, протекающий с ростом внутренней энергии (Δu>0). Если же от точки A идти по направлению стрелки вниз, то встречается адиабатный процесс расширения, идущий с уменьшением внутренней энергии (Δu<0). В области сжатия, двигаясь от точки B вверх, встречается адиабатный процесс сжатия, протекающий с ростом внутренней энергии (Δu>0), а при движении вниз от точки B – изобарный процесс сжатия, протекающий с уменьшением внутренней энергии (Δu<0). Таким образом, | 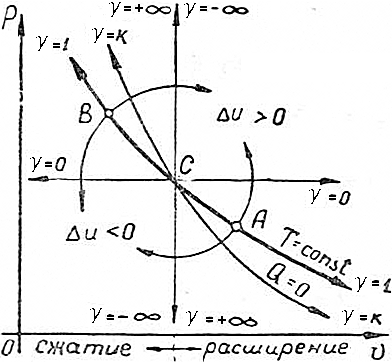 Рис. 4.22.
Рис. 4.22.
|
изотермический процесс делит политропные процессы, выходящие из одной точки, на две группы:
- политропные процессы, лежащие выше изотермы, как в области расширения, так и в области сжатия, протекают с ростом внутренней энергии газа (Δu>0);
- политропные процессы, лежащие ниже изотермы, как в области расширения, так и в области сжатия, протекают с уменьшением внутренней энергии газа (Δu<0).
| Рассмотрим подробнее изменение Δu при расширении. Проведём из точки 1 (рис.4.23) изотерму T1-const. Изотермы, лежащие выше неё, имеют большую температуру, изотермы, лежащие ниже – меньшую. Если политропный процесс лежит выше изотермы, температура газа в нём будет расти (т.к. при движении вдоль кривой этого процесса будут пересекаться изотермы всё больших температур), следовательно, внутренняя энергия в процессе увеличивается. Итак, в области от процесса подвода тепла при v=const до процесса расширения при T1=const выполняется условие Δu>0. Если политропный процесс расширения лежит ниже изотермы расширения, имеющей ту же начальную точку 1, то температура газа в политропном процессе падает (т.к. при движении вдоль кривой этого процесса пересекаются изотермы всё меньших температур), следовательно, внутренняя энергия в этом процессе будет уменьшаться. Итак, в области расширения | 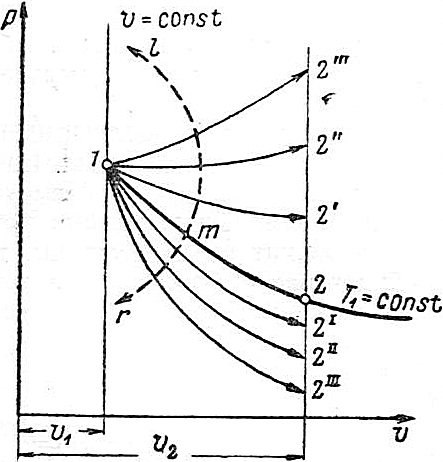 Рис. 4.23
Рис. 4.23
|
при T1=const до процесса отвода тепла при v=const будет выполняться условие Δu<0.
Рассмотрим, как меняется Δu=u2-u1 при движении от процесса T1=const к процессу подвода тепла при v=const (направление показано стрелкой ml) и при движении от процесса T1=const к процессу отвода тепла при v=const (стрелка mr). Пусть расширение газа происходит до объёма v2 (ограниченного, например, ходом поршня). При движении в направлении ml конечные температуры газа в политропных процессах возрастают, а начальная температура T1 останется постоянной. Следовательно, Δu растёт. Т.е. чем выше политропа по отношению к изотерме, проходящей через ту же начальную точку, тем больше растёт внутренняя энергия газа при одной и той же разности (v2-v1).
Аналогично можно показать, что чем ниже политропа относительно изотерме, проходящей через ту же начальную точку 1, тем более уменьшается внутренняя энергия газа при одной и той же (v2-v1).
Проанализируем зависимость знака теплоты от показателя 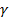 . При адиабатном процессе ( . При адиабатном процессе ( 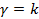 ) теплота не подводится и не отводится, Q=0 (жирная линия на рис.4.24). Очевидно, что во всех остальных процессах теплота участвует в процессе.
Если от точки C в области расширения двигаться вверх по стрелке, то встретятся изотермический и изобарный процессы расширения, протекающие с подводом внешнего тепла (Q>0).
Если двигаться от точки C вверх, то будем приближаться к предельному процессу v=const с отводом тепла ( ) теплота не подводится и не отводится, Q=0 (жирная линия на рис.4.24). Очевидно, что во всех остальных процессах теплота участвует в процессе.
Если от точки C в области расширения двигаться вверх по стрелке, то встретятся изотермический и изобарный процессы расширения, протекающие с подводом внешнего тепла (Q>0).
Если двигаться от точки C вверх, то будем приближаться к предельному процессу v=const с отводом тепла ( 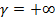 ).
В области сжатия, двигаясь от точки D вверх по направлению стрелки, будем приближаться к предельному процессу v=const с подводом тепла ( ).
В области сжатия, двигаясь от точки D вверх по направлению стрелки, будем приближаться к предельному процессу v=const с подводом тепла ( 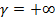 ); если двигаться вниз от точки D, то встретятся изотермический и изобарный процессы сжатия, протекающие с отводом тепла (Q<0). ); если двигаться вниз от точки D, то встретятся изотермический и изобарный процессы сжатия, протекающие с отводом тепла (Q<0).
| 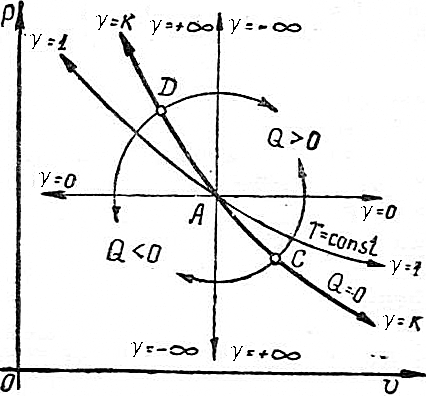 Рис. 4.24.
Рис. 4.24.
|
Таким образом, политропы, лежащие выше адиабаты в области расширения и сжатия протекают с подводом тепла (Q>0). Политропы ниже адиабаты в области расширения и сжатия – с отводом (Q<0).
Исследование зависимости Δu и Q от  позволяет выделить три типичных группы политроп I, II и III, положение которых в координатах v-p приведено на рис.4.25 (область расширения) и 4.26 (сжатия):
позволяет выделить три типичных группы политроп I, II и III, положение которых в координатах v-p приведено на рис.4.25 (область расширения) и 4.26 (сжатия):
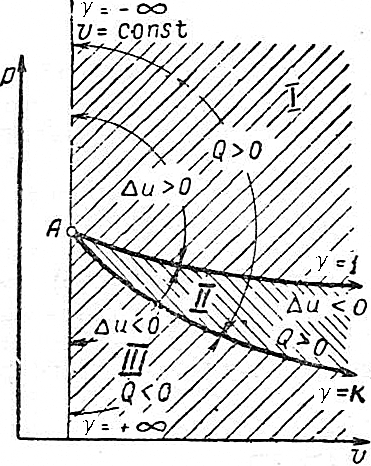 Рис. 4.25.
Рис. 4.25.
| 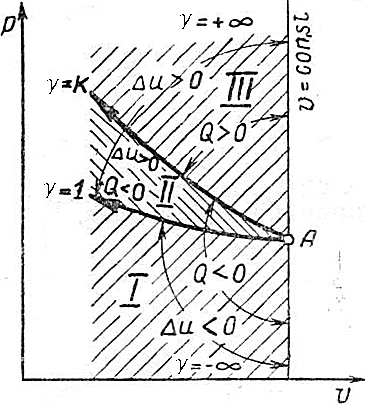 Рис. 4.26.
Рис. 4.26.
|
- первая группа политропных процессов располагается в области 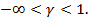
- вторая группа политропных процессов располагается между изотермическим и адиабатным процессами, т.е. в области 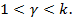
- третья группа политропных процессов располагается в области 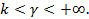
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|