
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Тема: Иррациональные уравнения и неравенства
20.11.20 Тема: Иррациональные уравнения и неравенства
Повторить стр.60-62 учебника
Выучить стр.63-68
Ознакомиться с видеоуроком по ссылке https://resh.edu.ru/subject/lesson/5569/conspect/159262/
Ознакомиться с образцами решения задач и переписать их в рабочую тетрадь.
№163(2, 3)
2) 3-х = ;
Возведём обе части уравнения в квадрат.
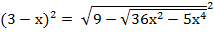 ;
;
9-6х+ 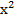 =
= 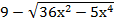 ;
;
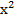 -6х=
-6х= 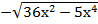 ;
;
Умножим на -1.
6х- 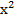 =
= 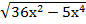 ;
;
Возведём обе части уравнения в квадрат.
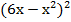 =
= 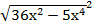 ;
;
36 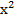 -12
-12 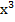 +
+ 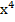 =
= 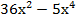 ;
;
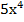 -12
-12 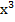 +
+ 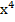 =0;
=0;
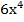 -12
-12 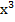 =0;
=0;
6 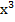 (х-2) = 0;
(х-2) = 0;
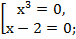
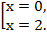
При возведении обеих частей уравнения в чётную степень возможно появление лишних корней. Обязательна проверка. Для этого подставим найденные значения в уравнение.
3-0= 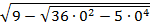 ;
;
3= 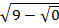 ;
;
3= 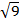 ;
;
3=3 - верное равенство. Тогда х=0 -корень данного уравнения.
3-2= 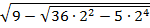 ;
;
1= 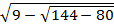 ;
;
1= 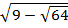 ;
;
1= 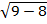 ;
;
1= 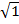 ;
;
1=1 - верное равенство. Тогда х=2 - корень данного уравнения
Ответ: х=0, х=2.
3) - =2;
Очевидно, что под корнями находится одинаковое буквенное выражение. Тогда выполним замену 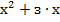 =а. Так как а находится под корнем арифметическим квадратным, то а
=а. Так как а находится под корнем арифметическим квадратным, то а 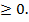
Получим 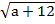 -
- 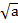 =2.
=2.
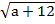 =
= 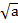 +2;
+2;
Возведём обе части уравнения в квадрат
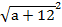 =
= 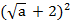 ;
;
а+12= а+2 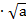
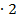 +4;
+4;
4 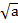 =8;
=8;
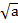 =2,
=2,
а=4.
Тогда 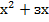 =4.
=4.
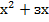 -4=0
-4=0
По обратной теореме Виета корни: х= -4, х=1.
Проверка.
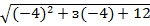 -
- 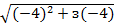 =2;
=2;
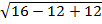 -
- 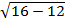 =2;
=2;
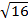 -
- 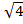 =2;
=2;
4-2 =2;
2=2 - верное равенство. Тогда х = -4 - корень.
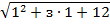 -
- 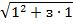 =2;
=2;
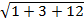 -
- 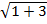 =2;
=2;
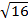 -
- 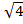 =2;
=2;
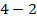 =2;
=2;
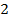 = 4 - верное равенство. Тогда х=1 - корень.
= 4 - верное равенство. Тогда х=1 - корень.
Ответ: х= -4, х=1.
№164(1) + = .
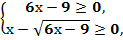
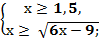
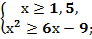
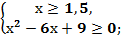
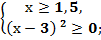
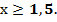
Обе части второго неравенства имеем право возвести в квадрат, так как с учётом первого неравенства х всегда положителен.
Возведём обе части уравнения в квадрат.
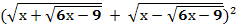 =6;
=6;
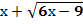 +2
+2 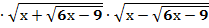 +
+ 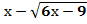 =6;
=6;
2х +2 =6;
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|