Хелпикс

Главная

Контакты

Случайная статья



Баранова Е.С.. Шаблонные интегралы. Этой теоремой надо пользоваться в первую очередь. Сначала смотрим чему эквивалентна подынтегральная функция, потом смотрим на шаблон. Как правило, ответ готов.



Баранова Е.С.

Шаблонные интегралы

 

  1. Для несобственных интегралов первого рода

,

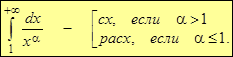где нижний предел может быть любым числом, большим нуля

 

  1. Для несобственных интегралов второго рода

,

где нижний предел может быть любым числом

 

Предельный признак сравнения в сокращенной форме:

Если при 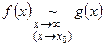  , то интегралы  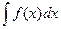 и 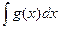 одинаковые в смысле сходимости (оба сходятся или оба расходятся). ( 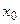–точка разрыва)

Этой теоремой надо пользоваться в первую очередь. Сначала смотрим чему эквивалентна подынтегральная функция, потом смотрим на шаблон. Как правило, ответ готов.

Пример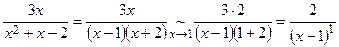         

Если пользоваться предельным признаком сравнения, то понадобятся:

 

  1. Теорема 1. Сумма бесконечно больших разного порядка эквивалентна беск. большой большего порядка.

Например,   

  1. Теорема 2. Сумма бесконечно малых разного порядка эквивалентна беск. малой меньшего порядка.

Например,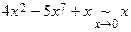

  1. Формулы эквивалентных бесконечно малых:

 

 

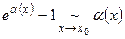
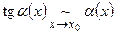
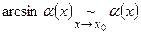
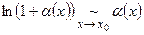
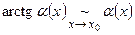
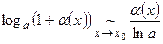
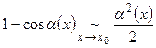
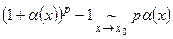
В этих формулах обязательно 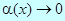 при .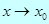
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.