
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Примеры решения задач. Решение.
Примеры решения задач
Пример 1. Исследовать сходимость ряда 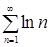
Решение. Применим необходимый признак сходимости.
 , следовательно ряд расходится, так как не выполнен необходимый признак сходимости.
, следовательно ряд расходится, так как не выполнен необходимый признак сходимости.
Пример 2. Исследовать сходимость ряда 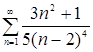
Решение.
Исходный ряд сравним с “эталонным” рядом 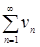 =
= 
Этот ряд сходится как ряд Дирихле, при  .
.
Поскольку 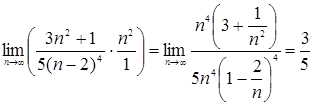 - конечное число, отличное от 0, то в силу второго признака сравнения заключаем, что исходный ряд сходится.
- конечное число, отличное от 0, то в силу второго признака сравнения заключаем, что исходный ряд сходится.
Пример 3. Исследовать сходимость ряда 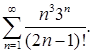
 |
Решение. Применим признак Даламбера. Записываем n-ый член ряда:
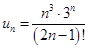
(n+1)-ый член получим, если в выражении 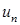 везде n заменим на (n+1):
везде n заменим на (n+1):
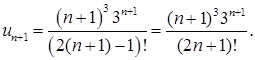
Найдем предел отношения:
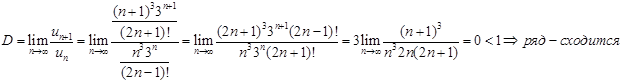
Пример 4. Исследовать сходимость ряда 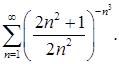
Решение.Здесь удобно применить радикальный признак Коши:

Следовательно, ряд сходится.
Пример 5.Исследовать сходимость ряда 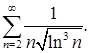
Решение.Рассмотрим функцию 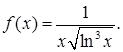
Она при x³2 положительная, непрерывная и монотонно убывает. (Заметим, что эта функция получается из выражения общего члена ряда при замене n на x). Можно применять интегральный признак. Исследуем сходимость несобственного интеграла:
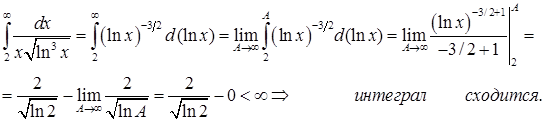
Из интегрального признака заключаем, поскольку несобственный интеграл сходится, то сходится и исследуемый ряд.
Пример 6.Исследовать сходимость ряда 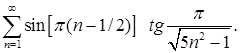
Решение.Данный ряд знакочередующийся, т.к.
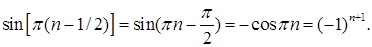
Исходный ряд можно переписать в виде 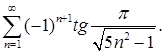
Рассмотрим сначала ряд, составленный из абсолютных величин исходного ряда: 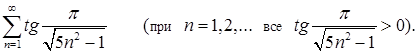
Сравним его с гармоническим рядом 1+ 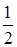 +
+ 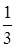 +…+
+…+ 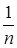 +…, о котором известно, что он расходится. Так как
+…, о котором известно, что он расходится. Так как 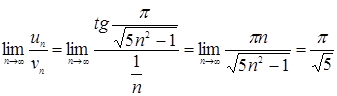 , то по второму признаку сравнения заключаем, что ряд из модулей расходится и, следовательно, исходный ряд абсолютно не сходится. Продолжим исследование с помощью признака Лейбница: члены исходного ряда удовлетворяют условиям: во-первых, монотонного убывания абсолютных величин членов ряда, во-вторых, общий член ряда стремится к нулю. В самом деле, в промежутке [0,
, то по второму признаку сравнения заключаем, что ряд из модулей расходится и, следовательно, исходный ряд абсолютно не сходится. Продолжим исследование с помощью признака Лейбница: члены исходного ряда удовлетворяют условиям: во-первых, монотонного убывания абсолютных величин членов ряда, во-вторых, общий член ряда стремится к нулю. В самом деле, в промежутке [0, 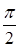 ] функция y = tg x монотонно возрастает, а при n = 1, 2, … выполняются неравенства, а также необходимое условие:
] функция y = tg x монотонно возрастает, а при n = 1, 2, … выполняются неравенства, а также необходимое условие:
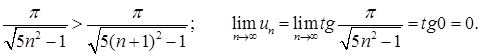
Окончательно заключаем, исходный ряд сходится условно.
Пример 7.Найти область сходимости степенного ряда 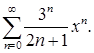
Решение. В развернутом виде ряд выглядит следующим образом
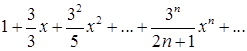
Коэффициенты ряда: 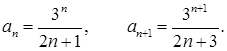
Найдем радиус сходимости 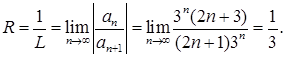
Заключаем, что интервал сходимости 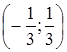 .
.
Исследуем далее сходимость степенного ряда в граничных точках интервала:
а) при x= 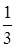 получим числовой положительный ряд:
получим числовой положительный ряд: 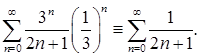
Этот ряд расходится, что видно из сравнения его с гармоническим рядом.
б) при x= 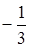 получим знакочередующийся ряд:
получим знакочередующийся ряд:
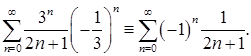
Члены этого ряда удовлетворяют условиям теоремы Лейбница:
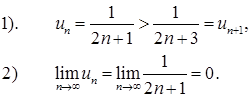
Знакочередующийся ряд сходится, т.е. при X = 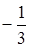 степенной ряд сходится и окончательно область сходимости степенного ряда определяется неравенствами
степенной ряд сходится и окончательно область сходимости степенного ряда определяется неравенствами 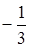 £ X <
£ X < 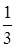 .
.
Пример. Исследовать сходимость ряда 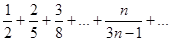
Найдем 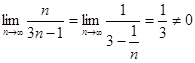 - необходимый признак сходимости не выполняется, значит ряд расходится.
- необходимый признак сходимости не выполняется, значит ряд расходится.
Пример. Исследовать на сходимость ряд 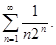
Т.к. 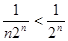 , а ряд
, а ряд 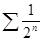 сходится ( как убывающая геометрическая прогрессия), то ряд
сходится ( как убывающая геометрическая прогрессия), то ряд 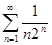 тоже сходится.
тоже сходится.
Пример. Определить сходимость ряда 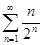 .
.
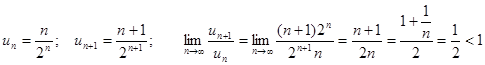
Вывод: ряд сходится.
Пример. Определить сходимость ряда 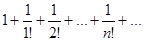
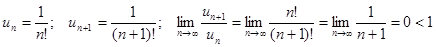
Вывод: ряд сходится.
Пример. Определить сходимость ряда 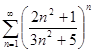 .
.
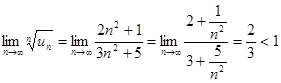
Вывод: ряд сходится.
Пример. Определить сходимость ряда 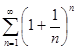 .
.
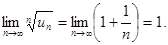
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|