
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Решение систем уравнений с двумя переменными.
Решение систем уравнений с двумя переменными.
Способ подстановки.
План решения:
1. В более простом уравнении выразить одну из переменных.
2. Выраженную переменную подставить в другое уравнение и решить его.
3. Полученное значение переменной подставить в первое действие и сосчитать.
4. Записать ответ.
Пример.
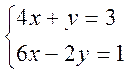
Решение:
1) 4х + у = 3
у = 3 - 4х
2) 6х – 2у = 1
6х – 2(3-4х) =1
6х – 6 + 8х = 1
14х = 7
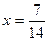
х = 0,5
3) у = 3 – 4 ∙ 0,5 = 3 -2 = 1
Ответ: (0,5; 1)
Решение систем уравнений с двумя переменными.
Способ сложения.
План решения:
1. Умножением всех членов уравнений на некоторые числа получить противоположные коэффициенты.
2. Сложить почленно уравнения системы и решить получившееся уравнение.
3. Найденное значение переменной подставить в более простое уравнение данной системы и найти значение другой переменной.
4. Записать ответ.
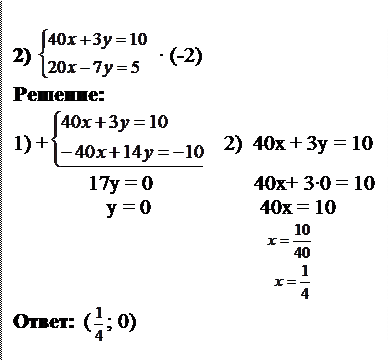 |
 Примеры:
Примеры:
1) 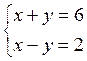
Решение:
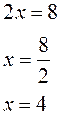 1)
1) 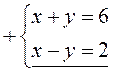 2) х + у = 6
2) х + у = 6
4 + у = 6
у = 6 – 4
у = 2
Ответ: (4; 2)
 |
3) 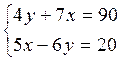 Переставим в первом уравнении:
Переставим в первом уравнении: 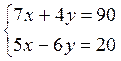
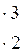
Решение:
1) 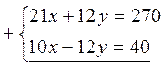 2) 7х + 4у =90
2) 7х + 4у =90
31 х = 310 7∙10 + 4у = 90
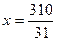 4у = 90 - 70
4у = 90 - 70
х =10 4у = 20
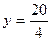
у =5 Ответ: (10; 5)
Решение задач с помощью систем уравнений
№ 1175
Решение:
1)
| Vсоб, км/ч | Vтеч, км/ч | V, км/ч | t, ч | S, км | |
| по течению | x | y | x+y | 3(x+y) | |
| против течения | x | y | x-y | 2(x-y) |
По условию задачи Sпо + Sпр = 240 км
Составляем уравнение: 3(х+у) + 2(х-у) = 240
5х + у = 240
2)
| Vсоб, км/ч | Vтеч, км/ч | V, км/ч | t, ч | S, км | |
| по течению | x | y | x+y | 2(x+y) | |
| против течения | x | y | x-y | 3(x-y) |
По условию задачи Sпр > Sпо на 35 км
Составляем уравнение: 3(х-у) - 2(х+у) = 35
х -5у = 35
3) Составляем систему уравнений:

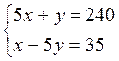 ∙ (-5)
∙ (-5) 
26у = 65
у = 2,5
x – 5y = 35
x – 5∙2,5 = 35
x = 35+12,5
x = 47,5
4) По смыслу задачи х>0, y>0, x>y. Этому условию удовлетворяет найденное решение. Значит, Vпо= х+у = 47,5 + 2,5 = 50 км/ч и
Vпр= х-у = 47,5 - 2,5 = 45 км/ч
Ответ:50 км/ч, 45 км/ч
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|