Хелпикс

Главная

Контакты

Случайная статья



ПРАКТИЧЕСКАЯ РАБОТА. по теме « Метод интервалов». Цель занятия.



ПРАКТИЧЕСКАЯ РАБОТА

по теме « Метод интервалов»

Формирование компетенций ОК2, ОК 6

Оборудование: компьютер, презентации, учебники:

  1. Богомолов Н.В. Математика. Уч. Пособие для ср. специальных уч. Заведений. М.: Высшая школа, 2009 г - 495 с
  2.  Алгебра и начала анализа: уч. для 10 – 11 кл общеобразовательных учреждений/ [ Ш.А. Алимов , Ю.М. Колягин и др.].-15 изд.- М.: Просвещение, 2007.- 387 с

Ход работы:

1. Познакомиться с теоретическим материалом

2. Сделать краткий конспект теоретического материала в  рабочих тетрадях (основные понятия, определения, формулы, примеры)

3. В тетрадях для практических работ выполнить самостоятельную работу или решить номера, которые указаны в работе.

4.  Сдать преподавателю тетради для практических работ.

Вид занятия.  практикум. Имеет целью изучение и первичное закрепление новых знаний по теме: Метод интервалов .

Цель занятия.

Учебная. Дать определение «Метода интервалов», повторить понятия решение линейных уравнений и систем линейных уравнений

Воспитательная: воспитание нравственного поведения. Расширение кругозора.

Обеспечение занятия. Наглядные пособия: ( примеры линейных уравнений и систем линейных уравнений)

1. Организационный момент

2. Изучение нового материала

Форма: эвристическая беседа. После повторения понятий «линейных уравнений и систем линейных уравнений» ;     

Литература дополнительная :

Богомолов Н.В. Практические занятия по математике. Уч. Пособие для ср. специальных уч. Заведений. М.: Высшая школа, 2009 г - 495 с

 Колмогоров «Алгебра и начала анализа» 10-11 класс

Ход занятия:

  1.  Решить неравенства:

1)  Х2 - 5х+ 6 > 0 à x1=2; x2= 3

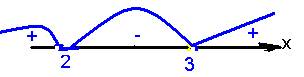
 Ответ: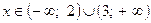

2) Х2 - 5х+ 6 < 0 à x1=2; x2= 3

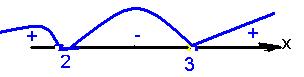Ответ: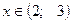

3)   Практическое Правило:

1.  Решить уравнение (найти корни уравнения);

2. На числовой прямой нанести полученные числа , учитывая, что если дано строгое неравенство (> , <), то на числовой прямой рисуем пустые кружки; эти числа в решение не входят, в ответе ставим круглые скобки.

3. На числовой прямой нанести полученные числа , учитывая, что если дано нестрогое неравенство ( 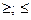), то на числовой прямой рисуем закрашенные точки; эти числа в решение входят, в ответе ставим квадратные скобки.

4. Пример: Решить неравенства:

а) Х2 - 5х+ 6 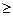   0 à  x1=2; x2= 3

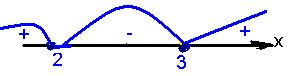
 Ответ: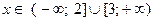

б) решить неравенство: Х2 - 5х+ 6 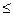   0 à x1=2; x2= 3

Ответ: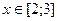

 Решить самостоятельно: 1) Х2 - 6х - 7 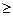   0 ; 2) Х2 - 6х - 7  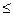  0;

3) Х2 - 6х - 7 < 0; 4) Х2 - 6х - 7 > 0; 5) Х2 - 6х - 9 < 0; 

6) Х2 - 10х < 0; 7) Х2 - 8х > 0; 8) Х2 - 8х - 9 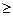   0;

 9) Х2 - 10х -116 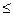   0; 10) Х2 - 4х  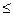 0

Консультанты проверяют   решение у студентов и на доске показывают верное оформление решения

САМОСТОЯТЕЛЬНАЯ РАБОТА ПО ТЕМЕ «РЕШЕНИЕ НЕРАВЕНСТВ»

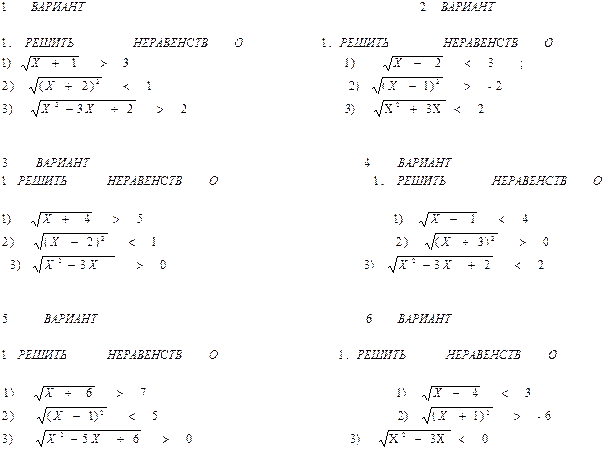Итог занятия.  

Домашнее задание: [2]. № 168; № 170 решить

 
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.