
- Автоматизация
- Антропология
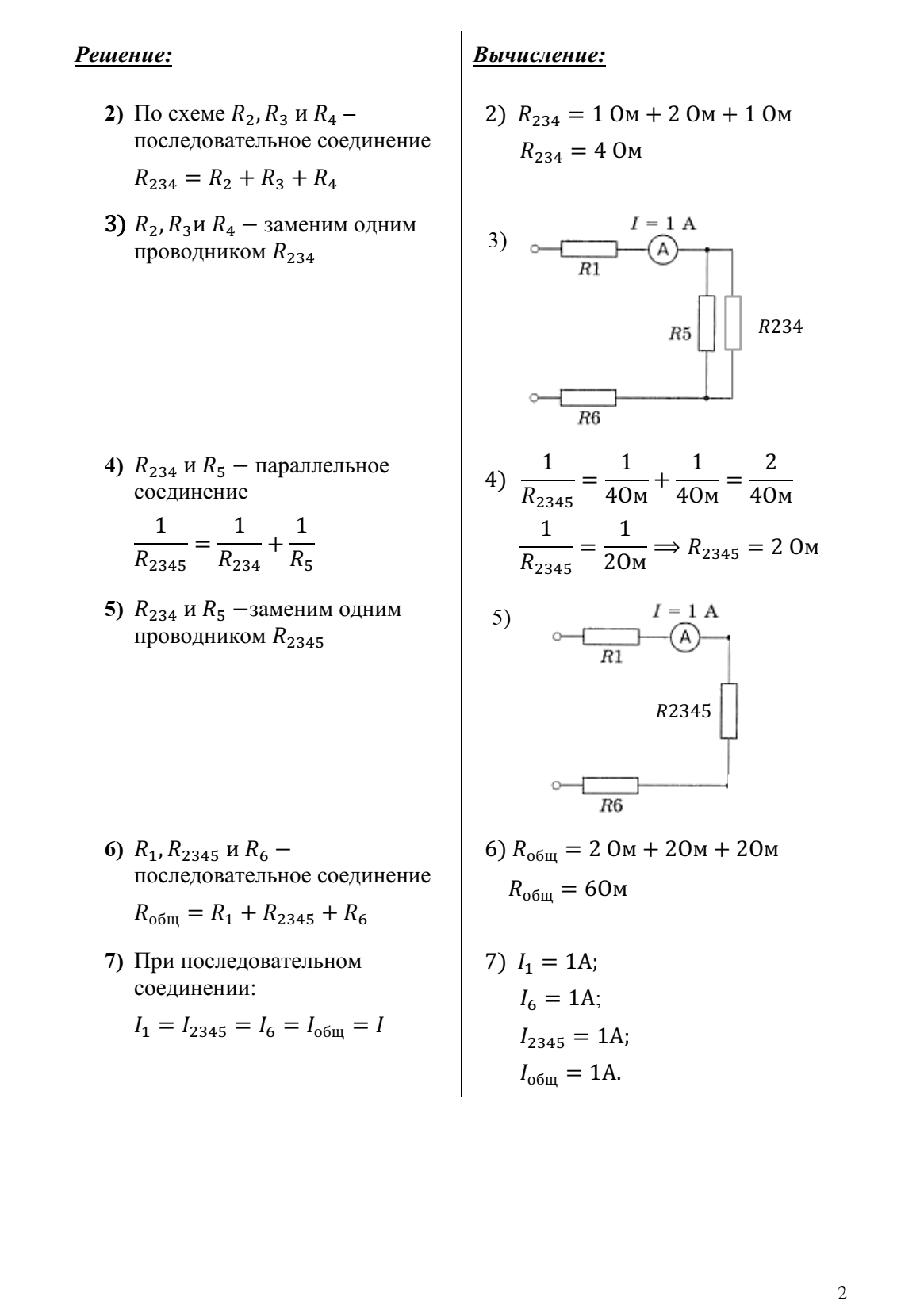
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
При решении задач на смешанное соединение проводников обычно составляют так называемые эквивалентные схемы, выделяя участки с последовательным и параллельным соединением.
При решении задач на смешанное соединение проводников обычно составляют так называемые эквивалентные схемы, выделяя участки с последовательным и параллельным соединением.
Пример 1.
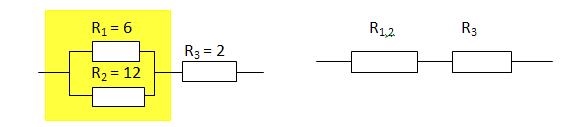
Сопротивление R1,2 заменило выделенный участок цепи, в котором два проводника соединены параллельно.
Тогда мы можем найти сопротивление этого участка с параллельным соединением проводников:
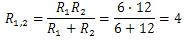
А теперь видно, что проводники R1,2 и R3 соединены последовательно. Общее сопротивление равно R = R1,2 + R3 = 4 + 2 = 6.
Пример 2.
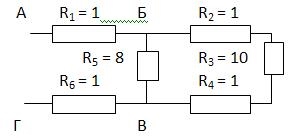
В данном случае нужно развернуть схему, двигаясь от точки к точке. Видно, что в точке Б схема разветвляется, а в точке В ветви соединяются. Таким образом, эквивалентные схемы будут иметь вид:
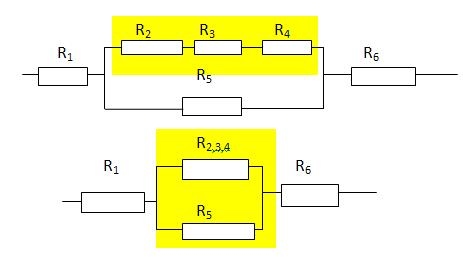
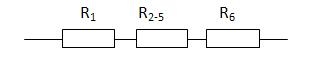
R2, R3 и R4 соединены последовательно. Поэтому R2,3,4 = R2 + R3 + R4 = 1 + 10 + 1 = 12
R2,3,4 и R5 соединены параллельно. Поэтому
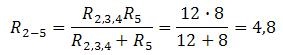
И в последней схеме проводники соединены последовательно. R = R2-5 + R1 + R6 = 1 + 4,8 + 1 = 6,8.
Пример 3. Найти распределение токов и напряжений в цепи.
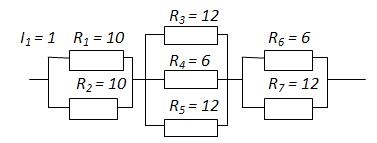
Решение.
Так как известны сила тока и сопротивление на первом участке, то можно найти напряжение на нем: U1 = I1 R1 = 1 ∙ 10 = 10 B.
Первый и второй проводники соединены параллельно. Значит, напряжение на них одинаково, т.е. U1 = U2 = 10 В. Так как первый и второй проводники имеют одинаковое сопротивление, то сила тока на них одинакова: I2 = 1 А. При параллельном соединении I1,2 = I1 + I2 = 2 А.
Участки 1-2, 3-4-5 и 6-7 соединены последовательно между собой, значит I3,4,5 = I6,7 = I1,2 = 2 A.
Найдем общее сопротивление участка 3-4-5:
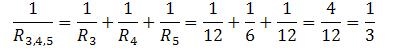
R3,4,5 = 3 Ом. Тогда можно найти напряжение на 3-4-5, при параллельном соединении оно одинаково на всех участках. U3,4,5 = I3,4,5 ∙R3,4,5 = 2 ∙ 3 = 6 В.
U3 = U4 = U5 = 6 В. Зная напряжение на каждом из участков и сопротивление, можно найти силу тока на каждом участке.
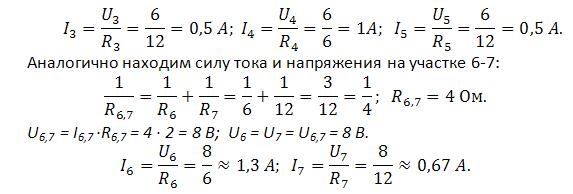
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|