Контакты

Случайная статья

Краевая задача для уравнения Пуассона

Краевая задача для уравнения Пуассона

Задание. Методом конечных разностей определить неизвестные значения сеточной функции 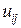в отмеченных точках (узлах):

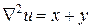– уравнение Пуассона внутри области,

краевые условия представлены на рис. 1.

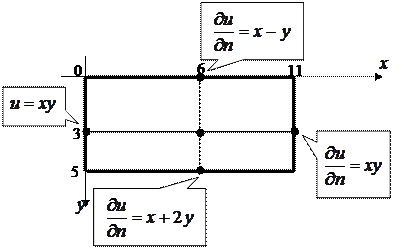
Рис. 1. К формулировке задания

1. Пронумеруем сеточные узлы и определим координаты вектора внешней 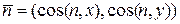нормали в граничных узлах, где заданы производные по нормали

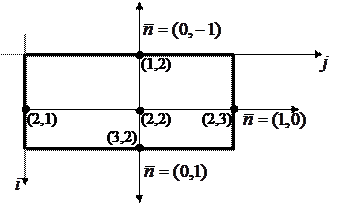
Рис. 2. К переходу к разностным уравнениям

2. Определим координаты узлов и шаги сеточного разбиения.

По горизонтали: , , , , ,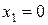

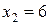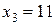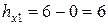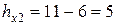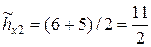
По вертикали: , , , , ,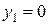

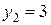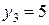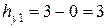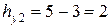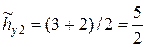
3.Заменим в узлах сеточной области исходные дифференциальные уравнения разностными.

В граничных узлах:

(1,2):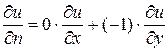

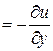
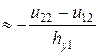
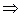
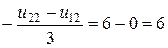
(2,1):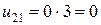

(2,3):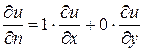

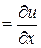
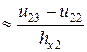
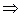
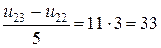
(3,2):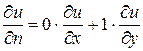

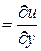
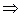
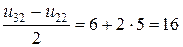
Во внутренних узлах:

(2,2):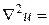

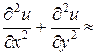
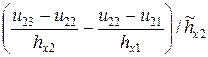
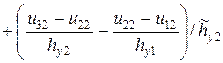
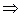
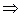
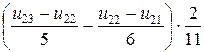
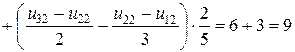
3.Разрешающая система разностных уравнений

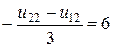
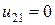
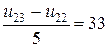
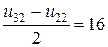
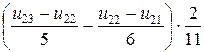
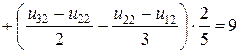
4. Решение разрешающей системы разностных уравнений

Для упрощения уравнения в узле (2,2) воспользуемся разностными уравнениями в граничных узлах.

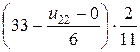
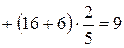или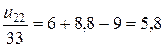

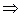
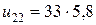
Из разностного уравнения в узле (1,2) следует

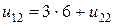
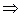
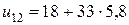
Из разностного уравнения в узле (1,2) следует

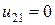
Из разностного уравнения в узле (2,3) следует

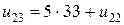
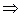
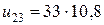
Из разностного уравнения в узле (3,2) следует

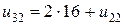
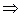
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.