
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Примеры решения заданий на преобразование выражений содержащих корни
Примеры решения заданий на преобразование выражений содержащих корни
Пример 1.Вычислить:

Решение
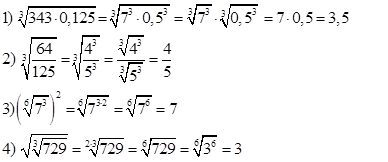
Пример 2. Внести множитель под знак корня в выражении: 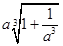 .
.
Решение.
Так как  , то
, то 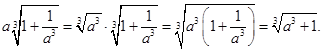
Пример 3. Вынести множитель из-под знака корня в выражении: 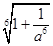 , где а<0.
, где а<0.
Решение.
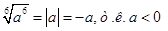 , то
, то  .
.
Пример 4. Выполнить действия: 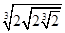 .
.
Решение.
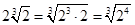 ;
; 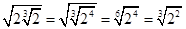 .
.
Отсюда: 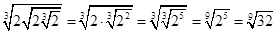 .
.
Пример 5– упростить и выполнить действия:
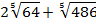
Решение
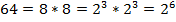
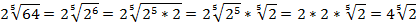
Разложим составное число 486 на простые множители:
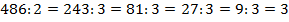
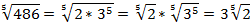
В результате преобразований получаем:
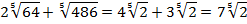
Пример 6 – выполнить умножение:
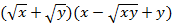
Решение
В данном случае нужно заметить другую формулу сокращенного умножения: 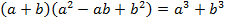 – сумма кубов;
– сумма кубов;
В нашем случае 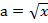 ,
, 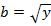 , получаем:
, получаем:
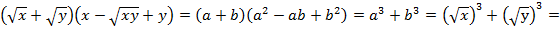
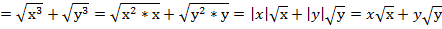
Комментарий: поскольку в заданном примере переменные х и у стояли под квадратным корнем, то они неотрицательны, значит, имеем право снять модуль.
Пример 7– сократить дробь: 
Решение
В данном случае также нужно воспользоваться формулой сокращенного умножения.
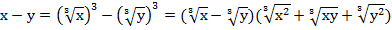
Таким образом, заданную дробь можно записать в следующем виде:
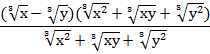
Чтобы иметь право сократить дробь, оговорим, что знаменатель ее не должен быть равен нулю, для этого х и у не должны одновременно быть равны нулю, тогда получаем ответ:
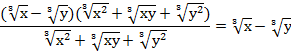
Пример 8– преобразовать выражение к виду 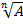 :
: 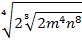
Решение
Внесем двойку под кубический корень:
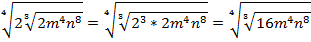
Согласно теореме о взятии корня из корня, перемножим показатели корней:
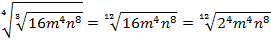
Согласно теореме о корне из произведения, получим:
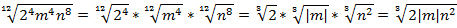
Пример 9 – упростить выражение: 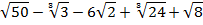
Решение
Представим все составные числа в виде простых чисел:
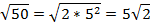
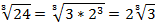
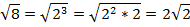
В результате преобразований получили выражение:

Пример 10 – вычислить: 
Решение
В знаменателе стоит выражение, распишем его по формуле квадрата разности:
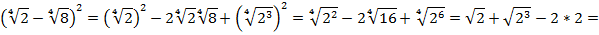
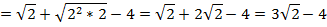
После преобразования получаем дробь:
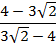
Вынесем в знаменателе минус за знак дроби:
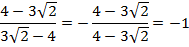
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|