Контакты

Случайная статья

Касательная плоскость и нормаль к поверхности

8. Касательная плоскость и нормаль к поверхности

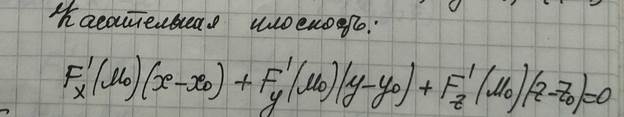
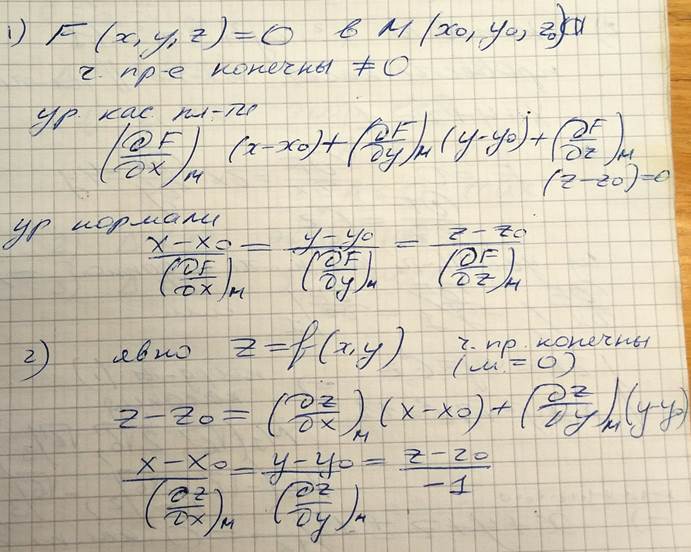
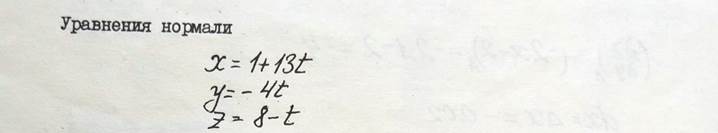
Пример. Найти уравнения касательной плоскости и нормали к поверхности

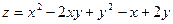
в точке М(1, 1, 1).

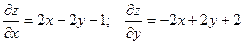
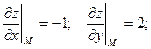
Уравнение касательной плоскости:

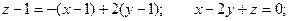
Уравнение нормали:

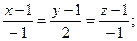
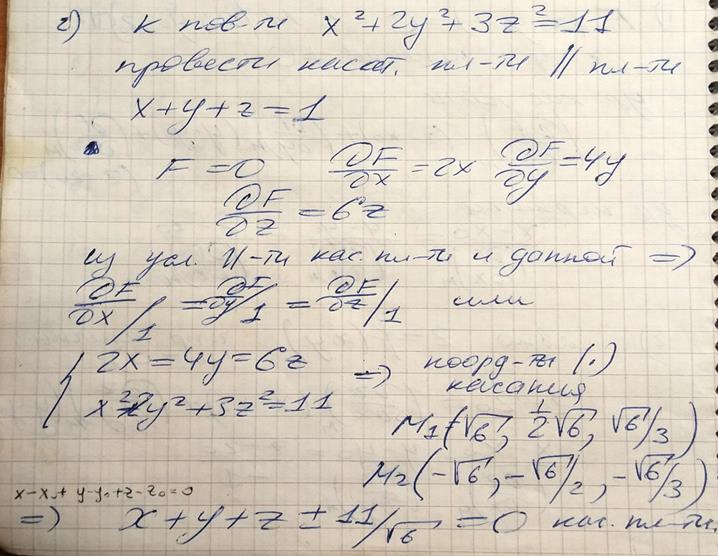
9. Производная функции в данном направлении. Градиент функции

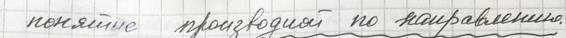
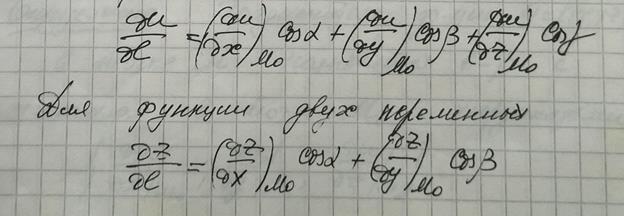
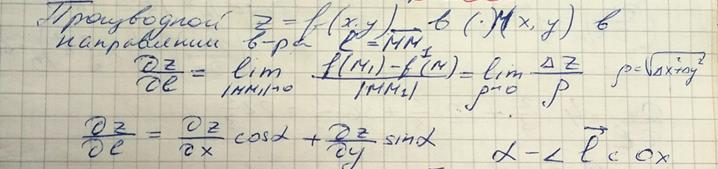
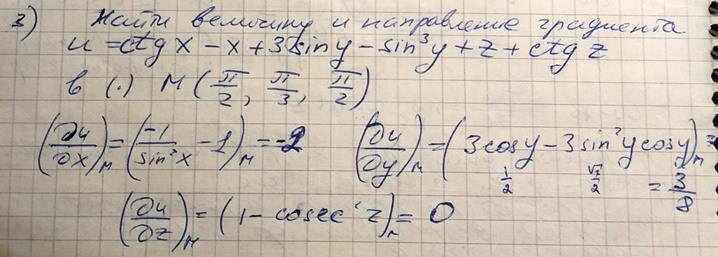
10. Приближенные вычисления с помощью полного дифференциала.

Пусть функция f(x, y) дифференцируема в точке (х, у). Найдем полное приращение этой функции:

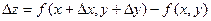
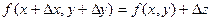
Если подставить в эту формулу выражение

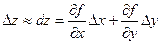
то получим приближенную формулу:

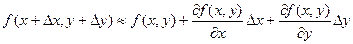
Пример. Вычислить приближенно значение , исходя из значения функции 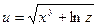при x = 1, y = 2, z = 1.

Из заданного выражения определим Dx = 1,04 – 1 = 0,04, Dy = 1,99 – 2 = -0,01,

Dz = 1,02 – 1 = 0,02.

Найдем значение функции u(x, y, z) =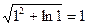

Находим частные производные:

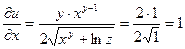
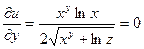
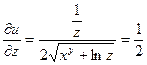
Полный дифференциал функции u равен:

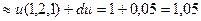
Точное значение этого выражения: 1,049275225687319176.

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.