Обратное z-преобразование. Обратное z-преобразование

Обратное z-преобразование

2.15. Обратное z-преобразование

Весьма важно уметь перейти не только от последовательности к ее z-преобразованию, но и, обратно, от z-преобразования к последовательности. Способ обратного перехода называется обратным z-преобразованием и формально определяется соотношением

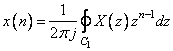(2.71)

В правой части этого равенства стоит контурный интеграл в z- плоскости по любому замкнутому контуру в области сходимости, охватывающему начало координат. Например, контуром интегрирования может быть окружность радиуса 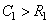, где 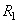— радиус сходимости z-преобразования (т. е. мы предполагаем, что последовательность 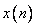физически реализуема).

Обратное z-преобразование можно найти несколькими способами:

1. Прямым вычислением интеграла (2.71) с использованием теоремы о вычетах.

2. Разложением 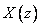на простые дроби.

3. Обычным делением числителя 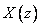на его знаменатель.

4. Разложением в степенной ряд.

Первый способ основан на известной теореме из теории функций комплексного переменного, утверждающей, что контурный интеграл (2.71) может быть вычислен непосредственно через вычеты:

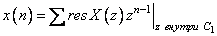(2.72)

Рассмотрим пример 4, в котором 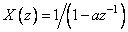. Из равенства (2.72) при 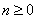получаем 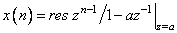, т. е. 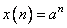, 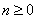. При 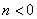кратный полюс z-преобразования находится в точке 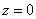. Прямое вычисление вычета в полюсе 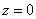дает 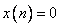при .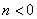

При использовании второго способа z-преобразование записывают в виде дроби (2.69) и представляют суммой

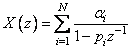(2.73)

С учетом того, что каждое слагаемое 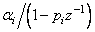имеет обратное z-преобразование вида 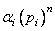, получим

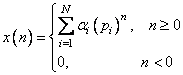(2.74)

Способы 3 и 4 здесь не рассматриваются. Читатель может познакомиться с ними в пособиях по z-преобразованию.

http://scask.ru/c_book_r_cos.php?id=19