Моделирование строения. в форме геодезического купола. Теоретическая часть

Моделирование строения

в форме геодезического купола

Выбирая архитектуру строений мы решили остановиться на сферической форме: шатры, юрты, иглу, и т.п. - самые древние и самые прочные жилища, придуманные человеком. Такие конструкции очень устойчивы и успешно противостоят природным стихиям. При самых сильных ветрах крышу не отрывает от стен. Поэтому, и на Марсе, где бушуют очень сильные ветра такая конструкция будет удачной.

Теоретическая часть

Первоначальная идея Найдя для образца подходящее изображение, мы нарезали равносторонних треугольников и начали собирать конструкцию, стараясь получить сферическую форму. Однако, к нашему удивлению, получалось плоское полотно, которое никак не хотело сворачиваться в шар. Пришлось искать дополнительную информацию как же нам построить подходящую модель.

Геодезический купол Оказалось такая конструкция носит официальное название – геодезический купол. Геодезический купол – гениальное изобретение американского изобретателя, инженера и архитектора Ричарда Бакминстера Фуллера. Фуллер разложил купольную конструкцию на треугольники, стороны которых располагаются на геодезических линиях, соединяющие две точки на криволинейной поверхности. Таким образом, геодезический купол - это сетка построенная из множества граней. Основой сетки стали треугольники, как самая стабильная и прочная структура из всех известных. И поэтому, структура из треугольников, очень прочна и обладает самонесущими способностями. Т.е. она "держит" сама себя, являясь целостной структурой. Чем больше граней мы будет использовано для построения, тем прочнее будет сетка, и более сглажена форма.

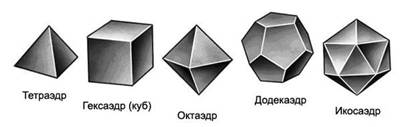Рассмотрев геодезический купол внимательно, становится заметно, что структура построения геодезической сетки не является хаотичной, а представляет собой строгую математическую модель. Эта модель берет свое начало из геометрии Платоновых тел - правильных многогранников, открытых учеными еще в далеком прошлом.

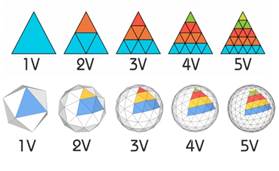Частота триангуляции Для расчета геокупола требуется понимать что такое «частота триангуляции». Это понятие подразумевает плотность разбивки купола на треугольники. Т.е. один и тот же купол можно «описать» разным количеством треугольников. Например, для менее плотной разбивки потребуется меньше треугольников, но с большей длиной ребра и форма будет более угловатой. Для более плотной разбивки потребуется большее количество треугольников с меньшей длиной ребра, но форма получится боле ровной и близкой к сферической.

В мире используется стандартное обозначение частоты латинской буковкой "V". Число значения частоты равняется количеству «рядов».

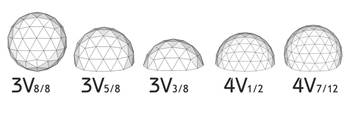Сечение сферы Следующий параметр, который следует знать при расчете геодезического купола – это значение сечения сферы. Если рассматривать сферу как целое, ее можно поделить на различное количество частей. Удобнее всего купол разбить по «рядам». У куполов с разной частотой триангуляции «V» - разное количество «рядов», поэтому сечение для них всегда индивидуальное.

12 3 Следующая ⇒