Контрольная работа

Министерство образования и науки Российской Федерации

ФГАОУ ВО «УрФУ имени первого Президента России Б.Н. Ельцина»

Институт новых материалов и технологий

Кафедра «Металлургия железа и сплавов»

Оценка работы______________

Руководитель от УрФУ_________/Спирин Н.А.

Контрольная работа

На тему: «Линейная регрессия от одного фактора. Определение коэффициентов уравнения регрессии»

Студент А.А. Кокшин

^{Подпись ФИО}

Группа НМТЗМ-102203

Екатеринбург 2021

Уравнение линии регрессии на плоскости в декартовых координатах имеет вид выражения 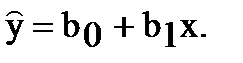(1).

(1)

Задачу метода наименьших квадратов аналитически можно выразить следующим образом:

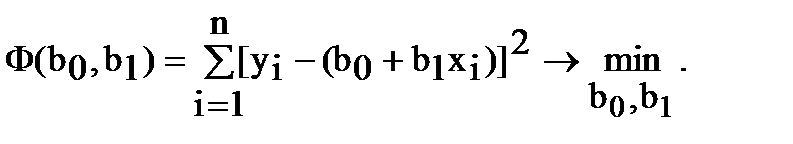(2)

Для решения этой задачи, как известно из математического анализа, необходимо вычислить частные производные функции Ф по коэффициентам b₀, b₁ и приравнять их нулю:

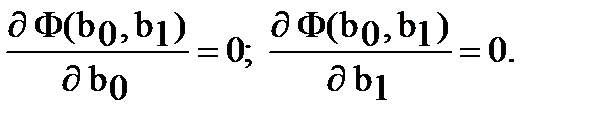(3)

Система нормальных уравнений в этом случае примет вид

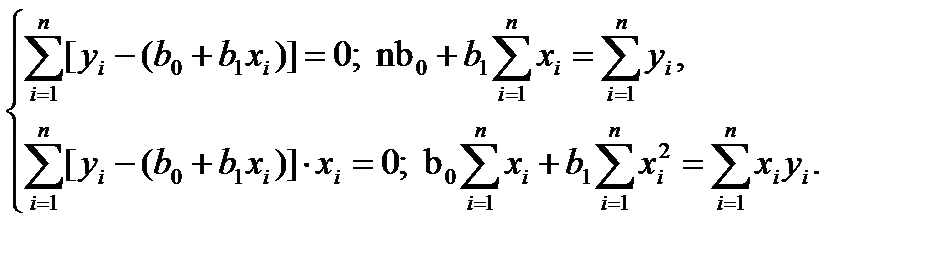(4)

Решение этой системы относительно b₀ и b₁дает

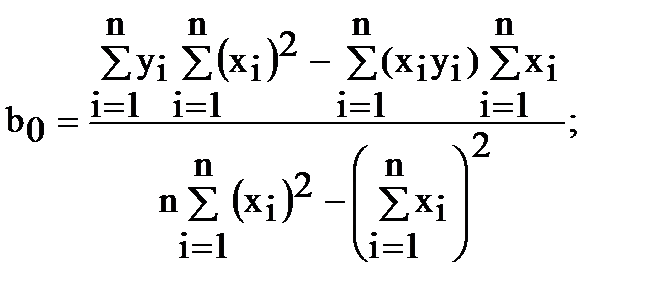(5)

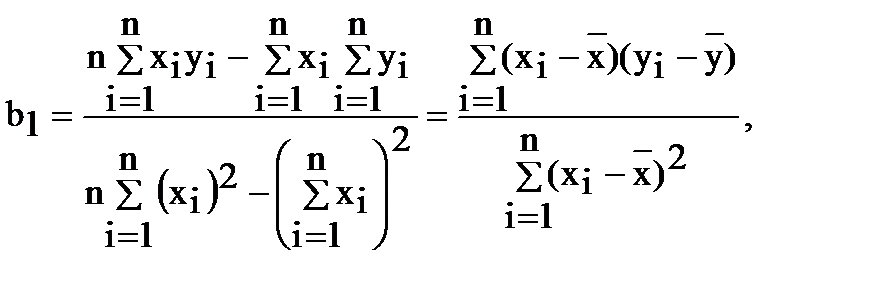(6)

т.е. для расчета b₀ и b₁ необходимо определить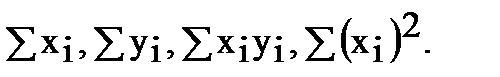

Коэффициент b₀ (свободный член уравнения регрессии) геометрически представляет собой расстояние от начала координат до точки пересечения линии регрессии с осью ординат, а коэффициент b₁ характеризует тангенс угла наклона линии регрессии к оси OX.

Если же определяют уравнение регрессии в виде

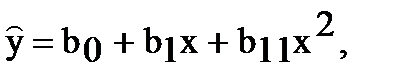
то система уравнений для нахождения b₀, b₁, b₁₁ будет иметь следующий вид:

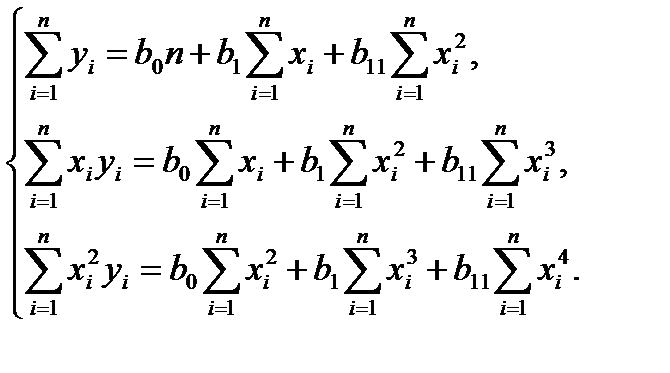(7)

Из уравнений (4) и (7) вытекает правило записи любых систем нормальных уравнений: необходимо записать столько уравнений в системе, сколько неизвестных коэффициентов содержится в искомом уравнении, всякий раз суммируя произведения членов исходного уравнения на переменную при искомом коэффициенте.