
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Идентификатор конференции. Код доступа 921394. Схема Горнера
Zoom
Идентификатор конференции
976 880 4436
Код доступа 921394
Схема Горнера
Удобный способ деления многочлена f(x) на двучлен х – с - схема Горнера.
Пусть f(x)= 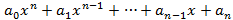 и g(x) =
и g(x) = 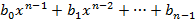 и пусть
и пусть
f(x) = (х – с) g(x) + r. ( 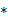 )
)
Сравнивая, коэффициенты при одинаковых степенях х в ( 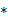 ), получаем: :
), получаем: : 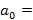
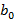 ,
, 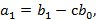
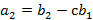 , …,
, …, 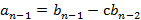 ,
, 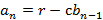 . Отсюда следует, что
. Отсюда следует, что 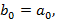
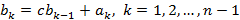 , т.е. коэффициент
, т.е. коэффициент 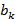 получается умножением предыдущего коэффициента
получается умножением предыдущего коэффициента 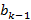 на с и прибавлением соответствующего коэффициента
на с и прибавлением соответствующего коэффициента 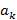 ; наконец,
; наконец, 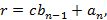 т.е. и остаток
т.е. и остаток 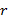 , равный f(с), получается по этому же закону. Оформим результаты в виде таблицы:
, равный f(с), получается по этому же закону. Оформим результаты в виде таблицы:
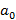
| 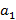
| … | 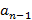
| 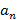
| |
| с | 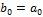
| 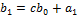
| … | 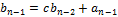
| 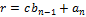
|
Схема Горнера позволяет найти значение многочлена f(x) при х = с, а именно, f(с)= r.
Пример.Разделить многочлен f(x) = 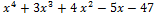 на х+3. Используем схему Горнера.
на х+3. Используем схему Горнера.
| -5 | -47 | ||||
| -3 | -17 |
Полученный результат означает, что f(x) =( х+3)( 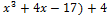 .
.
Также имеем f(-3)=4.
Пример. Разделить многочлен f(x) = 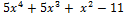 на ( х – 1).
на ( х – 1).
| -11 | |||||
Имеем f(x) = 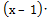
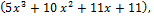
f(1)=0, т.е. х = 1 является корнем многочлена f(x).
Схема Горнера удобна при разложении данного многочлена f(x) по степеням двучлена х – с.
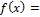
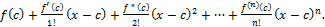
Это есть формула Тейлора для многочленов.
Деление по схеме Горнера 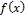 на х – с дает коэффициенты частного, которое в свою очередь надо делить на х – с и т.д. Вычисления удобно расположить в одну таблицу:
на х – с дает коэффициенты частного, которое в свою очередь надо делить на х – с и т.д. Вычисления удобно расположить в одну таблицу:
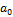
| 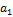
| … | 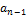
| 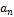
| |
| с | 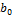
| 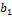
| … | 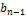
| 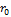
|
| с | 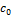
| 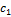
| … | 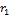
| |
| с | 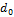
| 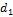
| … | ||
| … | … | … | |||
| с | 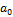
| 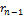
|
Здесь 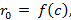
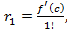
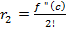 , …,
, …, 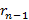 =
= 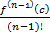 ,
, 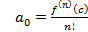 , откуда имеем
, откуда имеем 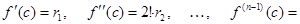
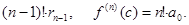
Таким образом, схема Горнера позволяет вычислить производные многочлена в заданной точке.
Пример.Найти значения многочлена f(x) = 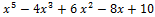 и его производных при х = 2.
и его производных при х = 2.
Используем схему Горнера.
| -4 | -8 | |||||
Имеем 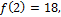
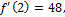
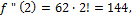
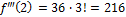 ,
,
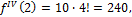
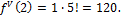
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|