Ключи, критерии оценивания заданий школьного этапа

Ключи, критерии оценивания заданий школьного этапа

Всероссийской олимпиады школьников

2020-2021 учебный год

Математика

8 класс

Максимальный балл – 35 баллов

Задача 1 (7 б.) Определите, какой цифрой оканчивается число 2¹⁹⁹⁹

Решение: Так как степени двойки заканчиваются на цифры 2, 4, 8, 6 с периодом 4 и 1999 = 4∙994 + 3, то 2¹⁹⁹⁹ оканчивается цифрой 8.

Ответ: 8

Балл	Критерии оценивания
	Любое полное верное решение
	Указано с периодом 4 чередование цифр: 2, 4, 8, 6, но неверно найдено, что число 2¹⁹⁹⁹ в данном периоде стоит на третьем месте, поэтому ответ получился неверным или допущена вычислительная ошибка
	Указано с периодом 4 чередование цифр: 2, 4, 8, 6
	Записан только ответ (без решения)
	Неверное решение или решение отсутствует

Задача 2 (7 б.) Белка за 20 минут приносит орех в гнездо. Какое расстояние она при этом пробегает, если без ореха белка бежит со скоростью 5 м/с, а с орехом – 3 м/с?

Решение:

Пусть х метров – расстояние от гнезда до места, в котором лежит орех.

Тогда 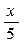секунд это время, которое потребуется белке для того, чтобы она добежала до ореха, а обратно она пробежит за 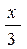секунд.

По условию задачи белка добежит до ореха и вернется обратно за 60 ∙ 20 = 1200 секунд. Составим уравнение:

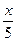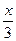+ = 1200

3х + 5х = 1200 ∙ 15

8х = 18000

х = 2250

значит, белка пробегает от гнезда до места, в котором лежит орех – 2250 метров.

Ответ: 2250 метров

Балл	Критерии оценивания
	Задача решена правильно
	Ход решения правильный, верно составлено уравнение, но при решении допущена вычислительная ошибка, которая привела к неверному ответу
	Записан только ответ (без решения)
	Неверное решение или решение отсутствует

Задача 3 (7 б.) Стрелок 10 раз выстрелил по стандартной мишени и выбил 90 очков. Сколько было попаданий в семерку, восьмерку и девятку, если десяток было четыре, а других попаданий и промахов не было.

Решение: Так как стрелок выбил 90 очков и из них за 4 раза набрал 40 очков, то в другие 6 раз он набрал оставшиеся 50 очков. Так как стрелок попадал лишь в семерку, восьмерку и девятку в остальные 6 выстрелов, то за три выстрела (по одному разу в семерку, восьмерку и девятку) он наберет 24 очка. Тогда за оставшиеся 3 выстрела надо набрать 26 очков, что возможно только при единственной комбинации цифр 7, 8, 9: 8 + 9 + 9 = 26. Таким образом, в семерку стрелок попал 1 раз, в восьмерку – 2 раза, а в девятку – 3 раза.

Балл	Критерии оценивания
	Задача решена верно, решение обосновано
	В решении указано, что стрелок за четыре попадания в десятку набрал 40 очков, поэтому, за оставшиеся 6 выстрелов ему осталось набрать 50 очков. Также указано, что стрелок точно по одному разу попал в семерку, восьмерку и девятку, что в сумме будет 24 очка, значит, останется «выбить» 26 очков. А дальше в решении не указано, что 26 очков можно набрать только при единственной комбинации цифр: 8 + 9 + 9.
	В решении указано, что стрелок за четыре попадания в десятку набрал 40 очков, указано, что за оставшиеся 6 выстрелов ему осталось набрать 50 очков, а дальше найдена верная комбинация чисел (8+9+9) методом перебора
	В решении выполнены только два шага: указано, что стрелок за четыре попадания в десятку набрал 40 очков и за оставшиеся 6 выстрелов ему осталось набрать 50 очков.
	Записан только ответ (без решения)
	Неверное решение или решение отсутствует

Задача 4 (7 б.) Один из внешних углов равнобедренного треугольника равен 34°. Найдите угол между основанием этого треугольника и высотой треугольника, проведенной из вершины угла при основании.

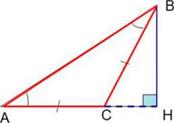Решение: Данный угол не может быть при основании равнобедренного треугольника, так как в этом случае сумма внутренних углов треугольника была бы больше 180°. Значит, данный угол находится при вершине. Тогда смежный с ним, внутренний угол треугольника, будет равен 146°, соответственно углы при основании будут по 17°. Значит, угол между основанием треугольника и высотой треугольника, проведенной из вершины угла при основании, будет равен: 180° – 90° – 17° = 73°.

Ответ: 73°

Балл	Критерии оценивания
	Задача решена верно (рассмотрены оба случая), решение обосновано, верно выполнен чертеж
	Задача решена верно (рассмотрены оба случая), решение обосновано, верно выполнен чертеж, но допущена вычислительная ошибка из-за которой был получен неверный ответ
	Задача решена (получен верный ответ), решение обосновано, верно выполнен чертеж, но рассмотрели только один случай, когда внешний угол равнобедренного треугольника расположен при вершине тупого угла и не рассмотрен случай, когда внешний угол расположен при основании треугольника
	Присутствует только половина решения задачи, т.е. рассмотрен случай когда внешний угол расположен при основании треугольника и доказано, что такое решение невозможно
	Верно выполнен чертёж и дан верный ответ
	Неверное решение или решение отсутствует

Задача 5 (7б.) Построить график функции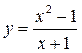

Решение:

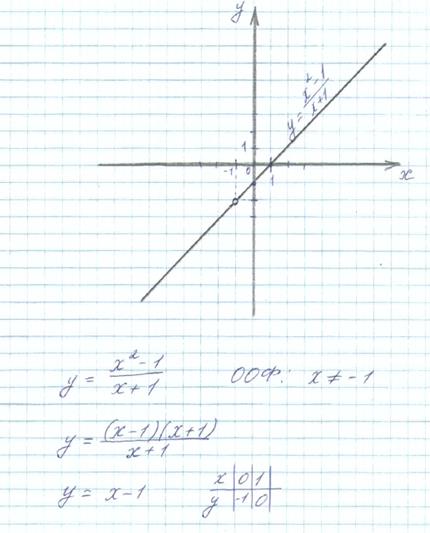
Балл	Критерии оценивания
	График построен верно, отмечена выколотая точка
6-5	Верно построен график, но есть недочеты в системе координат (не обозначены оси, или не указан единичный отрезок, или начало отсчета, или направление осей)
	Верно указана О.О.Ф., но график построен без выколотой точки
	Упрощена функция, построен график без выколотой точки и ООФ не указана
	Решение полностью неправильное или отсутствует