Основные понятия математической статистики

Лекция

Основные понятия математической статистики

Математическая статистика – раздел математики, изучающий математические приемы и методы обработки, систематизации и использования статистических данных для каких либо исследований.

Одно из основных понятий математической статистики – понятие совокупности. Совокупности можно разделить на генеральную и выборочную.

Генеральная совокупность – вся совокупность однотипных объектов, которая подлежит изучению.

Выборочная совокупность (выборка) – совокупность случайно отобранных объектов из генеральной совокупности.

Объемом совокупности называют количество элементов этой совокупности.

Объем генеральной совокупности обозначают N, а объем выборочной совокупности – n (n < N).

После обработки n объектов выборочной совокупности получают n чисел х₁, х₂, …, х_n, которые называются вариантами и образуют ряд вариант или простой статистический ряд.

Пусть в вариационном ряду варианта х₁ встречается n₁ раз, х₂ – n₂ раз, х_k – n_k раз.

Числа n₁, n₂, …, n_k называются частотами.

Также в математической статистике можно столкнуться с понятием относительной частоты, которая находится по формуле:

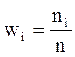
Из этих определений следуют равенства:

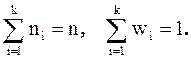
Статистическим распределением выборки называется соответствие между вариантами и частотами или относительными частотами.

x_i	x₁	x₂	…	x_k
n_i	x₁	x₂	…	x_k

x_i	x₁	x₂	…	x_k
w_i			…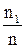

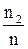
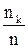
Еще одно важное понятие – эмпирическая функция распределения.

Эмпирической функцией распределения называется функция F^*(x), которая равна относительной частоте появления события (X < x):

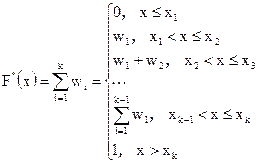
В процессе анализа статистических данных существенную роль играет геометрическая иллюстрация этих данных. Для наглядности строят разные графики статистических распределений, в частности полигон и гистограмму.

Полигон частот – ломанная, прямолинейные отрезки которой соединяют соседние точки (x_i;n_i) (i = 1, 2, …, k). Для построения полигона на оси абсцисс откладывают варианты x_i, а на оси ординат – соответствующие им частоты.

Полигон относительных частот – ломанная, прямолинейные отрезки которой соединяют соседние точки (x_i;w_i) (i = 1, 2, …, k). Для построения полигона на оси абсцисс откладывают варианты x_i, а на оси ординат – соответствующие им относительные частоты.

Гистограмма частот (относительных частот) – ступенчатая фигура, состоящая из прямоугольников с основанием – частичными интервалами длины h и высотами .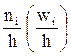

Построение статистических распределений выборки и их графическое изображение – это только первый шаг на пути решения задач математической статистики. Следующий шаг предусматривает нахождение числовых характеристик, которые в компактной форме выражают наиболее существенные особенности статистического распределения и служат оценками (приближенными значениями) неизвестных параметров распределения количественного признака генеральной совокупности.

Одна из таких характеристик – средняя выборочная.

Средняя выборочная (средняя арифметическая вариант) статистического распределения определяется по формуле

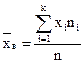
Если все n вариант разные, то формула приобретает такой вид:

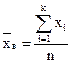
Пример. Из группы заводов одной из областей России случайным образом отобрано 30, по которым получены показатели основных фондов в миллионах рублей: 1, 2, 1, 3, 4, 1, 2, 2, 5, 3, 4, 3, 5, 4, 2, 3, 1, 3, 2, 2, 4, 3, 5, 3, 4, 2, 3, 2, 1, 3.

1. Определить объем выборки.

2. Составить статистическое распределение частот и относительных частот.

3. Составить распределение относительных частот.

4. Составить эмпирическую функцию распределения и построить ее график.

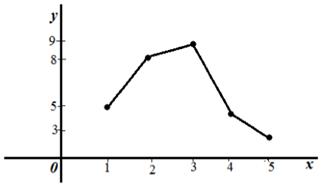
5. Построить полигон частот.

Решение

Объем выборки n = 30.

Данный ряд вариант запишем в виде вариационного ряда: 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3, 3, 3, 3, 3, 4, 4, 4, 4, 4, 5, 5, 5.

Варианты: х₁ = 1, х₂ = 2, х₃ = 3, х₄ = 4, х₅ = 5.

Частоты: n₁ = 5, n₂ = 8, n₃ = 9, n₄ = 5, n₅ = 3.

В итоге получается статистическое распределение частот:

x_i
n_i

Контроль: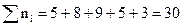

По формуле 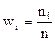последовательно вычисляем относительные частоты: w₁ = 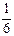, w₂ = 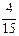, w₃ = 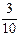, w₄ = 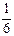, w₅ = .

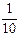Таким образом, статистическое распределение относительных частот имеет вид:

x_i
w_i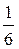

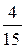
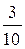
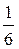
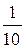
Построим эмпирическую функцию распределения.

Если 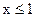, тогда нет ни одной варианты, меньшей от х, то есть 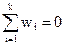и F^*(x) = 0.

Пусть 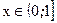. Тогда варианта х = 2 является меньшей от х, поэтому .

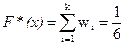Если х удовлетворяет двойному неравенству 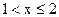, тогда меньшими от х являются варианты 1, 2, сумма относительных частот которых 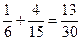. Поэтому для 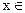(1; 2] .

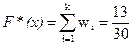Если х таково, что выполняется двойное неравенство 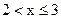, тогда меньшими от х являются варианты 1, 2, 3, сумма относительных частот которых 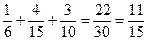. Поэтому для 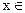(2; 3] .

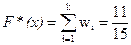Аналогично находим значение F^*(x) для интервалов (3; 4], (4; 5], (6;+ ).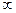

Таким образом, получаем:

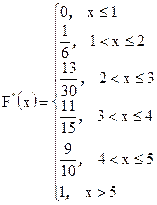
Построим график эмпирической функции распределения:

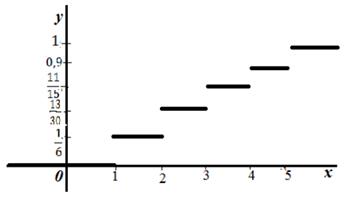
Построим полигон частот: