Представление объектов в пространстве вход-состояние-выход

Раздел 2. Математическое описание линейных непрерывных систем.

Лекция 3. Математические модели

Математическая модель – это математическое описание координат, параметров и функций, отображающих существенные свойства объекта, процесса или явления. Математическая модель объекта управления является основой для анализа и синтеза систем управления. В теории управления исследуются и рассматриваются не реальные системы, а их математические модели, поэтому результаты проводимых исследований и расчетов лишь приблизительно отражают свойства реальных систем. Чем точнее математическая модель отражает свойства реальной системы, тем точнее результаты проводимых расчетов.

Для получения математической модели системы управления необходимо дополнить уравнения объекта уравнениями исполнительных устройств, устройств измерения и управления.

Любая система автоматического управления может рассматриваться в виде совокупности отдельных связанных между собой элементов автоматики (чувствительных, промежуточных и исполнительных), взаимодействующих друг с другом и с объектом управления (регулирования). Разбиение системы автоматического управления на элементы позволяет ввести понятие функциональной схемы автоматической системы, приносящее большую пользу при рассмотрении принципа действия и аппаратурного состава систем управления. Однако для аналитического исследования процессов, происходящих при автоматическом управлении, необходимы уравнения, описывающие работу САУ. Ввиду сложности современных САУ уравнения, описывающие работу САУ, естественно получать, разбивая САУ на сравнительно простые части и составляя уравнения для каждой из таких частей по отдельности. При таком подходе расчленение САУ на функциональные элементы автоматики не всегда приносит пользу для математического описания работы системы управления. Объясняется это, прежде всего тем, что уравнения многих современных элементов автоматики достаточно громоздки; кроме того, различные элементы автоматики часто описываются однотипными уравнениями. Для математического описания работы САУ удобно разбивать ее не на функциональные элементы автоматики, а на динамические звенья. Поэтому вводится понятие динамического звена. Динамическим звеном называется часть системы управления, либо вся система, описываемая дифференциальным (или иным) уравнением определенного вида. Приведенное определение является общим. Под него подходит любой элемент автоматики, совокупность таких элементов и даже вся система автоматического управления в целом.

Существенно, что в отличие от функционального элемента автоматики, динамическое звено не обязательно является конструктивно или схемно-оформленным устройством. Например, в качестве динамических звеньев рассматриваются отдельные части функциональных элементов автоматики и объектов управления (обмотки возбуждения электрических генераторов, якорные обмотки электродвигателей, отдельные каскады усилителей и т. д.). Состояние любого динамического звена может быть охарактеризовано совокупностью соответствующих физических величин – обобщенных координат. Для электрических звеньев обобщенными координатами могут служить напряжения, токи и их производные; для механических – перемещения, скорости, ускорения. Многие звенья автоматических устройств обладают свойством направленного действия (однонаправленности), т. е. передают воздействие только в одном направлении от входа к выходу. В таких звеньях при изменении входной величины x_вх изменяется и выходная величина x_вых, изменения же выходной величины никак не сказывается на входной величине. Свойство однонаправленности практически реализуется за счет усиления входного сигнала звена по мощности. Пассивные звенья (рычаг, редуктор, пассивные электрические цепи и др.) свойством направленного действия не обладают. Уравнение звена должно быть составлено так, чтобы оно выражало зависимость (в динамическом процессе) между теми величинами, которые в схеме исследуемой системы указаны на выходе и входе данного звена, т.е. между величинами, представляющими воздействие данного звена на последующее по схеме звено и воздействие предыдущего звена на данное звено. Дифференциальное уравнение отдельного звена составляется по правилам, соответствующей технической науки. Звено иногда может иметь не одну входную величину, а несколько (например, при наличии дополнительных обратных связей). Кроме входной и выходной величин звена, которые выражают собой внутренние связи между звеньями данной системы, может учитываться также внешнее воздействие на данное звено. В большинстве случаев математическое описание динамических звеньев приводит к дифференциальным уравнениям того или иного вида. В результате физическая задача определения выходной величины звена при изменяющемся входном сигнале сводится к математической задаче отыскания решения дифференциального уравнения, описывающего работу звена.

Порядок составления дифференциального уравнения динамического звена

Порядок составления дифференциального уравнения звена:

1. Определяют входную (-ые) и выходную (-ые) величины (координаты) звена и устанавливают дополнительные факторы, от которых зависит выходная величина.

2. Используя основные законы той отрасли науки и техники, к которой относится исследуемое звено:

- законы Кирхгофа для электрических звеньев;

- законы Ньютона для звеньев механической природы;

- законы сохранения энергии и вещества для гидравлических и пневматических звеньев, составляют математическое описание звена в форме дифференциального уравнения.

3. Вводят те или иные упрощающие предположения (допущения) с целью упрощения исходного математического описания.

4. При необходимости осуществляют линеаризацию полученного дифференциального уравнения с целью получения линейного дифференциального уравнения звена.

Линеаризация — (от лат. linearis — линейный), один из методов приближённого представления замкнутых нелинейных систем, при котором исследование нелинейной системы заменяется анализом линейной системы, в некотором смысле эквивалентной исходной. Методы линеаризации имеют ограниченный характер, т. е. эквивалентность исходной нелинейной системы и её линейного приближения сохраняется лишь для ограниченных пространственных или временных масштабов системы, либо для определенных процессов, причём, если система переходит с одного режима работы на другой, следует изменить и её линеаризированную модель. Применяя линеаризацию, можно выяснить многие качественные и особенно количественные свойства нелинейной системы.

Для примера покажем, как построить модель двигателя постоянного тока, используя законы механики и электротехники. Вход этого объекта - напряжение якоря u(t) (в вольтах), выход - угол поворота вала ω(t) (в радианах).

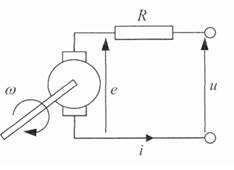
Рисунок 3.1 – Двигатель постоянного тока

Сначала вспомним некоторые «житейские» знания об электродвигателях. Вал двигателя начинает вращаться, когда приложено напряжение питания. Если напряжение не меняется, угловая скорость вращения ω(t) (в радианах в секунду) остается постоянной, при этом угол φ(t) равномерно увеличивается.

Чем больше напряжение, тем быстрее вращается вал. Если зажать вал рукой (или подключить нагрузку, например, заставить двигатель вращать турбину), скорость вращения постепенно уменьшается до нового значения, при котором вращающий момент двигателя будет равен моменту сопротивления (нагрузки). Пока эти моменты равны, скорость вращения остается постоянной и ее производная равна нулю.

Теперь переведем эти рассуждения на строгий язык математики. Угловая скорость вращения ω(t) вычисляется как производная от угла поворота вала φ(t), то есть t

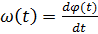Соответственно, угол φ(t) - это интеграл от угловой скорости. В механике уравнение вращательного движения обычно записывают в виде

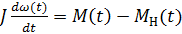где M(t) - вращающий момент (измеряется в Нм), M_Н(t)- момент нагрузки (возмущение, также в Нм). Буквой J обозначен суммарный момент инерции якоря и нагрузки (в кг м²). Величина момента инерции говорит о том, насколько легко «разогнать» двигатель (чем больше момент инерции, тем сложнее «разогнать»).

Перейдем к электротехнике. В нашем случае момент M(t) - это электромагнитный момент двигателя, который вычисляется по формуле

М(t) = С_м Ф i(t),

где С_м – коэффициент, Ф – магнитный поток, создаваемый обмоткой возбуждения (измеряется в веберах); i(t) – ток якоря (в амперах), который может быть найден из уравнения

u(t) = e(t) + R – i(t),

где e(t) – электродвижущая сила (ЭДС) якоря (в вольтах) и R – сопротивление якорной цепи (в омах). В свою очередь, ЭДС рассчитывается через магнитный поток и частоту вращения:

e(t) = С_ωФω(t),

где С_ω – коэффициент. Вводя новые постоянные k₁ = С_м Ф и k₁=С_ωФ, можно записать модель двигателя в виде системы уравнений

(1)

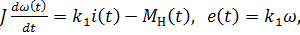
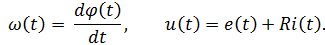
Модель (11) описывает связи реальных сигналов в системе, ее внутреннее устройство.

Часто нам достаточно знать, как будет реагировать объект на заданный входной сигнал (управление). При этом его внутреннее устройство нас не очень интересует, то есть мы рассматриваем объект в качестве «черного ящика». Подставив второе уравнение из системы (11) в третье, найдем i(t) и подставим в первое уравнение. Переходя к переменной φ(t), получаем:

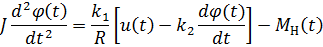
или, перенося все члены, зависящие от φ(t), в левую часть равенства

(2)

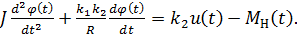
Это дифференциальное уравнение второго порядка, связывающее вход u(t) и нагрузку М_H(t) с выходом φ(t) . В сравнении с системой (1), все внутренние сигналы исходной модели (e(t) и i(t) были исключены из уравнений. Поэтому уравнение (2) называется уравнением «вход- выход».

Порядком модели называют порядок соответствующего дифференциального уравнения. В данном случае мы получили модель второго порядка.

В этом разделе на простом примере мы посмотрели, как на основе физических законов строятся математические модели объектов управления. Как правило, они представляют собой дифференциальные уравнения. В дальнейшем мы будем использовать готовые модели объектов управления, предполагая, что они были кем-то получены ранее (например, предоставлены заказчиком).

Представление объектов в пространстве вход-состояние-выход

Для того, чтобы было легче исследовать модель объекта, желательно привести ее к некоторому стандартному виду, для которого уже есть готовые общие решения. Таким «стандартом» в теории управления считается система дифференциальных уравнений первого порядка, которая называется нормальной формой Коши.

Рассмотрим снова модель электродвигателя, считая, что М_H(t) = 0 (нагрузки нет). Вспомнив. что ω(t) = φ’(t), можно записать равенство (2) см. прошлую лекцию, в виде системы:

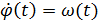
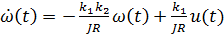
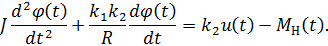
Эта система дифференциальных уравнений первого порядка быть записана в матричной форме:

(3.1)

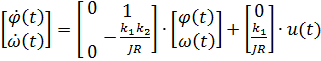
Значения φ(t) и ω(t) определяют состояние двигателя в момент времени t. Это значит, что зная их значения в некоторый момент времени t₀ и входной сигнал u(t) при всех t > t₀ можно рассчитать поведение объекта для любого последующего момента. При этом предыдущие значения φ(t), ω(t) и u(t) (при t< t₀) не играют никакой роли. Поэтому φ(t) и ω(t) называются переменными состояния, а вектор 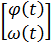- вектором состояния.

В теории управления принято обозначать вектор состояния через x(t), вход объекта (сигнал управления) - через u(t). Тогда уравнение в матричной форме (3.1) может быть записана в виде:

(3.2)

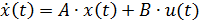
где 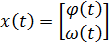, , 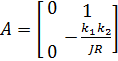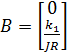. Уравнение (4) связывает вход u(t) и вектор состояния x(t), поэтому оно называется моделью вход-состояние.

(3.3)

Полная модель объекта в пространстве состояний содержит еще одно уравнение - уравнение выхода, которое показывает, как формируется выход объекта y(t):

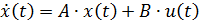
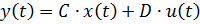
Эта модель называется моделью вход-состояние-выход. Выходная координата для двигателя постоянного тока - это угол поворота вала:

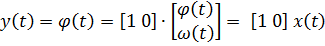
так что 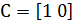и D=0. Если же в качестве выхода принять угловую скорость, то .

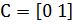С помощью модели (3.3), изменяя матрицы С и D, можно принять за выход любую линейную комбинацию переменных состояния и входа. Во многих практических задачах выход - это одна или несколько переменных состояния, которые мы можем измерить.

Поскольку момент инерции J, сопротивление якоря R и коэффициенты k₁, и k₁ не зависят от времени, матрицы А, В, С и D в модели (3.3) - постоянные. Такие объекты называются стационарными, в отличие от нестационарных объектов, параметры которых изменяются во времени.

Запись моделей в единой форме (3.3) позволяет отвлечься от смысла переменных состояния и исследовать системы разной природы стандартными методами, которые хорошо разработаны и реализованы в современных компьютерных программах.