Контакты

Случайная статья

Кручение круглого прямого бруса

Кручение

Кручением называется такой вид нагружения бруса, при котором в его поперечных сечениях возникает только один внутренний силовой фактор – крутящий момент.

Считаем, что брус находится в равновесии и применяем метод сечений.

Правило знаков: при рассмотрении любой из оставленных частей бруса со стороны сечения внешние моменты, действующие по ходу часо-

вой стрелки – положительны, а против – отрицательны.

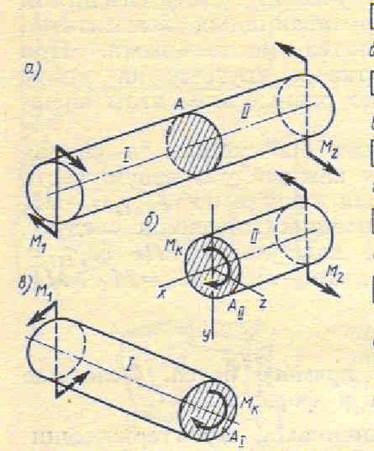
М_К = ∑М_скрМ_скр = М₁, М₂ – скручивающие

моменты

Кручение круглого прямого бруса

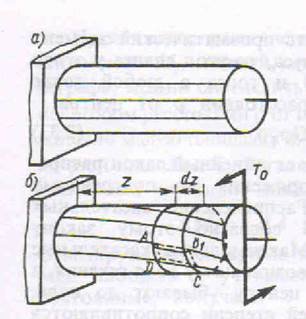
Если свободный конец бруса нагрузить скру-

чивающим моментом, то брус деформируется (скручивается) и линии на цилиндрической поверхности принимают вид винтовых линий.

φ – угол закручивания;

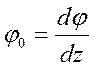- относительный угол закручивания.

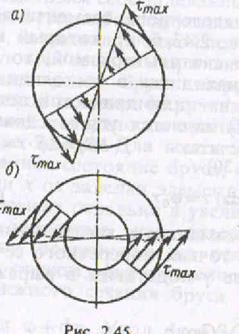
τ_max = G · φ₀ · r – максимальное касательное

напряжение в крайних точках попереч-

ного сечения бруса;

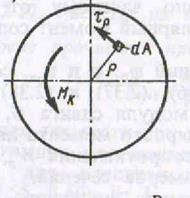
τ_ρ= G · φ₀ · ρ – касательное напряжение в точке

поперечного сечения на расстоянии ρ от

центра.

Это равенство выражает линейный закон распределения касательных напряжений по поперечному сечению при кручении.

М_К = G · φ₀ · J_P,

где J_P – полярный момент инерции сечения,

мм⁴, см⁴, м⁴.

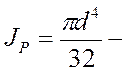для круга;

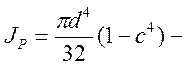для кольцевого сечения,

где 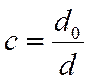, d₀ – наружный диаметр кольца

d – внутренний диаметр кольца.

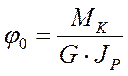- относительный угол закручивания,

рад/м, рад/мм;

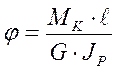- полный угол закручивания, рад.

G · J_P – жесткость сечения бруса при

кручении.

Условие прочности при кручении:

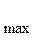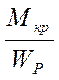τ = ≤ [τ ],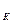

где W_Р– полярный момент сопротивления

W_P= 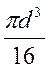-для круглого сечения;

W_Р = 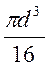(1 – с⁴),где с = 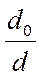- для кольца.

Три вида расчетов при кручении:

1) Проектный:

W ≥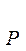

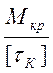
2) Расчет допускаемой нагрузки:

[M_кр] ≤ W_P[τ_к]

3) Проверочный:

τ _max = 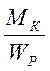≤ [τ_к]

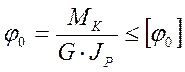- условие жесткости при круче-

нии.

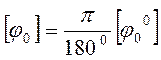- перевод градусов в радианы.

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.