
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Комплексные числа. записанными в алгебраической форме.
Комплексные числа
Определение. Комплексным числом z называется упорядоченная пара чисел (а,b), над множеством которых по определенным правилам можно производить следующие операции: сложение , умножение, деление, возведение в степень результаты которых также являются комплексными числами.
Определение. Алгебраической формой комплексного числа zназывается выражение 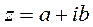 , где a и b – действительные числа, i – мнимая единица, которая определяется соотношением:
, где a и b – действительные числа, i – мнимая единица, которая определяется соотношением:

При этом число a называется действительной частью числа z (a = Re z (real)), а b- мнимой частью (b = Im z (imaginarius)).
Если a =Re z =0, то число z будет чисто мнимым, если b = Im z = 0, то число z будет действительным.
Определение. Числа 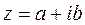 и
и 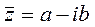 называются комплексно – сопряженными.
называются комплексно – сопряженными.
Определение. Два комплексных числа 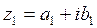 и
и 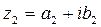 называются равными, если соответственно равны их действительные и мнимые части:
называются равными, если соответственно равны их действительные и мнимые части:

Определение. Комплексное число равно нулю, если соответственно равны нулю действительная и мнимая части.
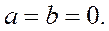
Действия с комплексными числами,
записанными в алгебраической форме.
Основные действия с комплексными числами вытекают из действий с многочленами.
1) Сложение и вычитание – раскрытие скобок, перед которыми стоит знак «плюс» или «минус» и приведение подобных слагаемых.
Пример. 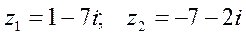
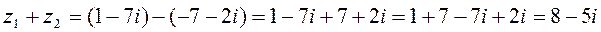
2) Умножение – умножение двучлена на двучлен: каждое слагаемое в первой скобке на каждое слагаемое во второй скобке. Также учитываем, что i2=-1.
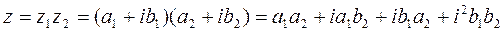
Пример. 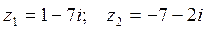
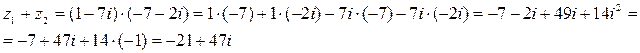
В случае умножения комплексно – сопряженных чисел используем формулу сокращенного умножения «разность квадратов» (a+b)(a-b)=a2-b2 и 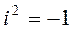 .
.
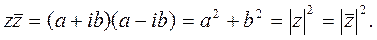
3) Деление – чтобы выполнить деление двух комплексных чисел, необходимо записать их в виде дроби, умножить числитель и знаменатель на число, комплексно сопряженное знаменателю, и выполнить действия в числителе и знаменателе, результат записать в виде комплексного числа.
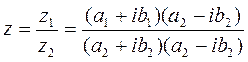
Пример. 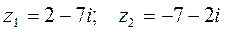
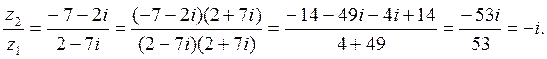
4) Возведение в степень – используем определение степени:
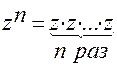
Пример. Вычислить 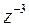 , если
, если 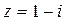 .
.
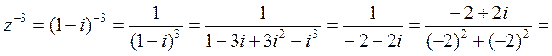
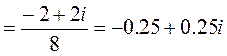 .
.
Замечание. Введение понятия комплексного числа позволяет решать квадратные уравнения, у которых дискриминант отрицательный, на множестве комплексных чисел.
Пример. Решить квадратное уравнение на множестве комплексных чисел:
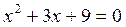 ;
;
a=1, b=3,c=9;
D=d2-4ac=32-4·1·9=9-36=-27
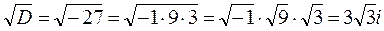
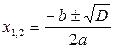
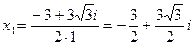
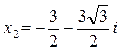
Ответ: 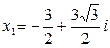 ;
; 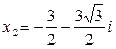
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|