
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Задания к коллоквиуму по разделу «Элементы проективной геометрии»
Задания к коллоквиуму по разделу «Элементы проективной геометрии»
- В чем состоит предмет проективной геометрии?
- Какие свойства фигур называются проективными?
- Какие свойства фигур сохраняются при проективных преобразованиях?
- Назовите 3-4 свойства фигур, меняющиеся при проективных преобразованиях.
- Что такое «расширенная евклидова прямая»?
- Назовите несколько отличий расширенной евклидовой прямой от обычной прямой.
- Как задать несобственную точку?
- Что такое «расширенная евклидова плоскость»?
- Назовите несколько отличий расширенной евклидовой плоскости от обычной плоскости.
- Как задать несобственную прямую?
- Сколько несобственных точек у расширенной прямой?
- Сколько несобственных прямых у расширенной плоскости?
- Как могут располагаться две прямые на расширенной плоскости?
- Какие плоскости пересекаются по несобственной прямой?
- Почему были введены несобственные элементы?
- Какое отображение двух множеств называется сюръективным?
- Дайте определение п-мерного проективного пространства.
- Назовите модели проективной прямой.
- Назовите модели проективной плоскости.
- Как задать проективную систему координат на прямой?
- Сколько несобственных точек можно взять, задавая проективную систему координат на прямой?
- Как задать проективную систему координат на плоскости?
- Сколько несобственных точек можно взять, задавая проективную систему координат на плоскости?
- Каковы проективные координаты точки
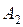 в проективном репере
в проективном репере 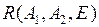 на прямой?
на прямой? - Каковы проективные координаты точки
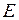 в проективном репере
в проективном репере 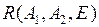 на прямой?
на прямой? - Каковы проективные координаты точки
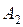 в проективном репере
в проективном репере 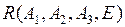 на плоскости?
на плоскости? - Каковы проективные координаты точки
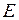 в проективном репере
в проективном репере 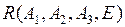 на плоскости?
на плоскости? - Сохраняется ли отношение «лежать между» на расширенной прямой? Почему?
- Постройте точку М(-2:2) в репере
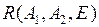 на прямой.
на прямой. - Постройте точку М(-1:2:1) в репере
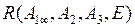 на плоскости.
на плоскости. - Сформулируйте малый принцип двойственности.
- Сформулируйте большой принцип двойственности.
- Сформулируйте двойственное для утверждения: две прямые на плоскости определяют единственную точку.
- Сформулируйте двойственное для утверждения: любые две плоскости определяют единственную прямую.
- Сформулируйте прямую теорему Дезарга (полная формулировка). Сделайте чертеж.
- Сформулируйте прямую теорему Дезарга (краткая формулировка). Сделайте чертеж.
- Сформулируйте обратную теорему Дезарга (полная формулировка). Сделайте чертеж.
- Сформулируйте обратную теорему Дезарга (краткая формулировка). Сделайте чертеж.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|