План работы обучающихся, находящихся на дистанционном и электронном обучении на 23.05.2020 Класс: 9

План работы обучающихся, находящихся на дистанционном и электронном обучении на 23.05.2020 Класс: 9

Предмет	Ф.И.О педагога	класс	дата	Тема урока	Учебник (стр.,§)	Задания для дистанционного обучения (для тех, у кого нет Интернета ит. д)	Задания для электронного обучения	Сроки выполнения	Электронная почта педагога телефон
Информатика	Аветян Э.Л.		23.05.2020	Алгебра логики. Практические задания.	Стр.125-134	Просматриваем видео. Разбираемся с практической частью. Задание № 2 в конце практической части прислать фото или скриншот.	Видео. Практическая часть. Построение таблиц истинности для логических выражений https://www.youtube.com/watch?time_continue=137&v=vWLGKw0U5TU&feature=emb_logo	до 25.05	teppoevaelya1904@yandex.ru личное сообщение в контакте

Практическая часть.

1. Посмотреть видео по ссылке (всё хорошо и подробно разобрано).

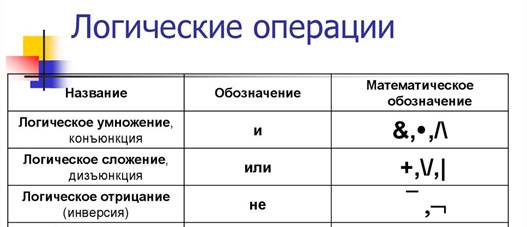
2. Выучить условные обозначения

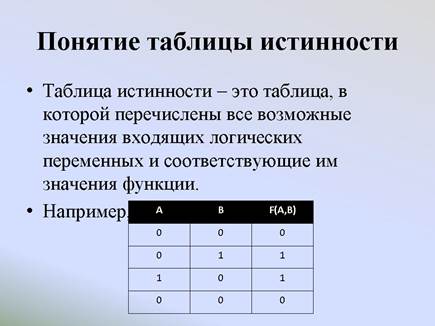
Понятие таблицы истинности: таблица истинности — это таблица, в которой перечислены все возможные значения входящих логических переменных и соответствующие им значения функции.

Определим для начала алгоритм наших действий:

Определить число переменных.
Определить число строк в таблице истинности.
Записать все возможные значения переменных.
Определить количество логических операций и их порядок.
Записать логические операции в таблицу истинности и определить для каждой значение.
Подчеркнуть значения переменных, для которых F = 1.

Число строк определяются по формуле: N = 2^q, где q — количество переменных.

Порядок действий в таблицах определяется следующим образом:

Действия в скобках.
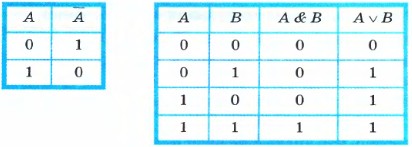
Инверсия (отрицание или черта над буквой) (Если А =0, то отрицание А=1)
Конъюнкция (умножение · , &, /\). (здесь уместно вспомнить 8 класс 0*0=0, 0*1=0,

1*0=0, 1*1=1)

Дизъюнкция (сложение +, \/, |) (0+0=0, 0+1=1, 1+0=1, 1+1=1)

Задание 2.

На основе полученных сведений постройте таблицу истинности для логического выражения.

(A ∨ B) & ( A ∨ B)