ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 26. Краткие теоретические сведения

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 26

Тема:Геометрическое преобразование пространства: параллельный перенос и симметрия в пространстве

Краткие теоретические сведения

В алгебре рассматриваются различные функции. Функция 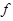каждому числу 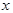из области определения функции ставит в соответствие некоторое число 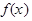– значение функции 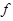в точке 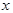. В геометрии рассматриваются функции, у которых другие области определения и множества значений. Они каждой точке ставят в соответствие точку. Эти функции называются геометрическими преобразованиями.

С помощью геометрических преобразований определяются такие важные геометрические понятия, как равенство и подобие фигур.

Виды геометрических преобразований:

1) Центральная симметрия

2) Симметрия относительно плоскости (зеркальная симметрия)

3) Параллельный перенос

4) Осевая симметрия

Преобразование пространства, при котором каждая точка пространства отображается на точку, симметричную ей относительно точки 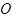, называется центральной симметрией пространства относительно точки 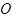. При этом точка 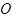отображается на себя и называется центром симметрии.

Примерами центральной симметрии являются: автомобильное колесо, окружность, куб, шар, снежинка, цветок и тд.

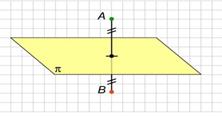
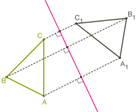
Определение. Преобразование пространства, при котором каждая точка пространства отображается на точку, симметричную ей относительно плоскости 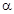, называется симметрией пространства относительно плоскости 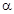. Плоскость 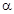называется плоскостью симметрии.

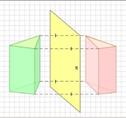
Примеры симметрии относительно плоскости:

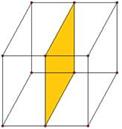
Определение. Параллельным переносом на вектор называется такое преобразование пространства, при котором любая точка 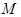отображается на такую точку 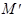, что выполняется векторное равенство 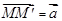. Это перенос (движение) всех точек пространства в одном и том же направлении, на одно и то же расстояние

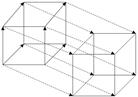
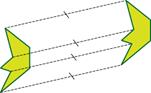
Примеры параллельного переноса:

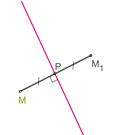
Определение. Осевая симметрия — это симметрия относительно проведённой прямой (оси).

12 Следующая ⇒