Лабораторно-практическая работа №5-повтор№1!!!!!!!!!!!!!!!!!!!!!!!

Лабораторно-практическая работа №5-повтор№1!!!!!!!!!!!!!!!!!!!!!!!

«Элементарные логические схемы»

Цель работы:

- изучение принципов работы элементарных логических схем;

- составление таблиц истинности на основании работы схем.

Материальное оснащение:

- персональный компьютер (процессор Pentium с ОЗУ не менее 8 Мб);

- монитор с разрешающей способностью не менее 800х600;

- видеокарта, работающая в режиме 800х600 с цветностью не менее 65 тысяч цветов;

- операционная система: Windows 95, Windows 98, Windows NT или Windows ХР;

- манипулятор "мышь";

- система моделирования «Начала электроники».

Ход работы.

1. Теоретическая часть

Уточним смысл логических величин 1 и 0, т. е. напряжение 5 В это 1 и нулевой уровень напряжения это 0, разомкнутое состояние ключа соответствует 0, а замкнутое — 1.

1.1. Схема И

В соответствии с рисунком 1 электрическая схема реализует функцию И.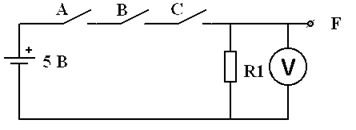

Рисунок 1 - Схема И

Эта простая схема состоит из трех ключей, источника питания, сопротивления нагрузки R и вольтметра V. Проследим теперь за напряжением на выходе схемы (т. е. в точке F) относительно земли при замыкании и размыкании контактов ключей в соответствии с рисунком 1.

Вольтметр покажет напряжение 5 В только после того, как будут замкнуты контакты всех трех ключей (A и В и С), или 1 появится на выходе только тогда, когда А и В и С находятся в состоянии 1. Вольтметр покажет напряжение 0 В, если А или В или С или несколько этих ключей одновременно будут разомкнуты, или на выходе появится 0, тогда А или В или С или несколько этих ключей одновременно находятся в состоянии 0. Можно составить таблицу истинности, в которой будут перечислены состояния трех входных переменных и в которой реализуются 2³ = 8 состояний рассмотренной схемы. Таблица истинности состояний схемы И приведена в таблице 1.

Таблица 1

C B A	F
0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1

Для обозначения схемы И используют символ в соответствии с рисунком 2.

Рисунок 2 - Символ для схемы И

Так как схема в соответствии с рисунком 1 реализует функцию И для единиц на входе, то ее можно представить с помощью одного символа в соответствии с рисунком 2. Однако при этом не следует забывать, что схема, обозначенная таким символом, будет одновременно реализовывать функцию ИЛИ для нулей на входе. Тот факт, что F является функцией И от переменных A, В, С, на языке булевой алгебры записывается в следующем виде:

F = AxBxC = A*B*C = A/\B/\C = A&B&C, или сокращенно F = АВС.

Эту связь можно также выразить словами, говоря, что функция F равна 1, если и А, и В, и С равны 1.

1.2. Схема ИЛИ

В соответствии с рисунком 3 электрическая схема реализует функцию ИЛИ для единиц на входе, которая состоит из ключей, источника питания, вольтметра и резистора.

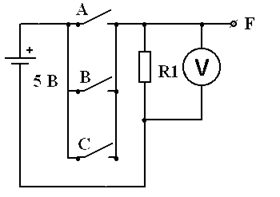
Рисунок 3 - Схема ИЛИ

Если замкнуть контакты ключей А или В или С или нескольких ключей одновременно, то источник питания через один или несколько ключей присоединится к выходу и вольтметр покажет напряжение 5 В, которое соответствует логической 1. И только в том случае, когда контакты ключей А и В и С будут разомкнуты, вольтметр покажет на выходе 0 В, т. е. напряжение, соответствующее логическому 0. Таблица истинности различных состояний схемы И приведена в таблице 2.

На выходе появится 1, когда А или В или С или несколько этих ключей одновременно будут находиться в состоянии 1. На выходе схемы появится 0, когда ключи А и В и С находятся в состоянии 0, т. е. схема ИЛИ для единиц на входе реализует функцию И для нулей на входе. Функция F является функцией ИЛИ для входных переменных А, В и С, и этот факт в терминах булевой алгебры выражается следующим образом:

F = A+B+C = A\/B\/C,

или же словами: функция F равна 1, если А или В или С или несколько названных переменных одновременно равны 1. Знак + указывает, что мы имеем здесь дело с функцией ИЛИ

Таблица 2

C B A	F
0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1

Для обозначения схемы ИЛИ используют символ в соответствии с рисунком 4. Этот символ показывают, что это схема, которая реализует функцию ИЛИ для единиц на входе и функцию И для нулей на входе.

Рисунок 4 - Символ для схемы ИЛИ

1.3. Схема НЕ

В соответствии с рисунком 5 электрическая схема реализует функцию НЕ.

Ключ А является двухполюсным, и когда он находится в нулевом положении (т. е. в состоянии 0), источник питания присоединяется к выходу. В нулевом состоянии ключа напряжение на выходе равно 5 В и соответствует логической 1. При переводе ключа в состояние 1 связь между источником питания и выходом нарушается и вольтметр измеряет нулевое напряжение, т. е. на выходе схемы появляется логический 0.

Рисунок 5 - Схема НЕ

Таблица истинности различных состояний схемы И приведена в таблице 3. Если ключ находится в состоянии 0, то на выходе появляется 1, а если в состоянии 1, на выходе появляется 0.

Таблица 3

A	F
0 1	1 0

Для обозначения схемы НЕ используют символ в соответствии с рисунком 6.

Рисунок 6 - Символ для схемы НЕ

Если функция НЕ используется в комбинации со схемой И или ИЛИ, ее указывают с помощью небольшого кружка в соответствии с рисунком 6. Выходной сигнал рассматриваемой схемы равен значению функции НЕ входного сигнала, что в булевой алгебре обозначается как

F = A (произносится: F есть НЕ A).

Функция НЕ указывается с помощью черты отрицания, располагающейся над А. Часто эта черта заменяется апострофом (А`). Если сигнал А активен, то А = 1 и А`=0. Если сигнал А неактивен, то A = 0 и A` = 1.

1.4. Схема И-НЕ

Схема И-НЕ является комбинацией схем НЕ и И. В соответствии с рисунком 7 электрическая схема реализует функцию И-НЕ.

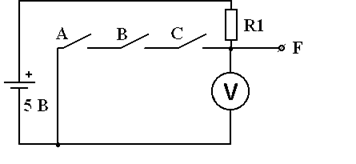
Рисунок 7 - Схема И-НЕ

Если замкнуть контакты ключей А, В и С, т. е. перевести их в состояние 1, на выходе схемы появляется 0. На выходе появится 1, если А или В или С или несколько этих ключей одновременно будут разомкнуты, т. е. будут находиться в состоянии 0. Таблица истинности различных состояний схемы И приведена в таблице 4.

Таблица 4

C B A	F
0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1

Из этой таблицы следует, что схема И-НЕ обеспечивает функцию И-НЕ для единиц на входе, так как на ее выходе появляется 0, если А и В и С равны 1. Именно функция НЕ обеспечивает на выходе не 1, как в случае схемы И, а 0. С ее помощью происходит инверсия сигнала, т. е. 1 превращается в 0. Для нулей на входе схема И-НЕ ведет себя как функция ИЛИ-НЕ, так как если один или несколько ключей одновременно находятся в состоянии 0, то на выходе схемы появляется 1.

Для обозначения схемы И-НЕ используют символ в соответствии с рисунком 8, где показано, что функция НЕ действительно обозначается кружком, расположенным на выходе.

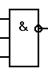
Рисунок 8 - Символы для схемы И-НЕ

Схема И-НЕ реализует функцию И-НЕ для единиц на входе, что на языке булевой алгебры записывается следующим образом:

______ ______

F = AxBxC = A*B*C,

т. е. F равна 0, если А и В и С равны 1.

Схема обеспечивает функцию ИЛИ-НЕ для нулей на входе, т. е. на языке алгебры логики

_ _ _

F = A + B + C,

или F равна 1, если А или В или С или несколько этих переменных одновременно равны 0.

______ _ _ _

F = A*В*С = А+В+С или дополнение произведения переменных равно сумме их дополнений (теорема Де Моргана). Схема И-НЕ реализует функцию И-НЕ для единиц на входе и функцию ИЛИ-НЕ — для нулей на входе.

1.5. Схема ИЛИ-НЕ

В соответствии с рисунком 9 электрическая схема реализует функцию ИЛИ-НЕ.

Если А или В или С или несколько этих ключей одновременно замкнуты, т. е. проводят ток, то на выходе схемы появится 0. И наоборот, если А и В и С разомкнуты, т. е. находятся в состоянии 0, то на выходе появится 1.

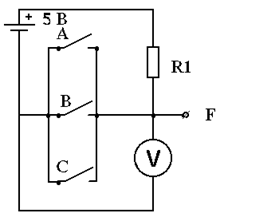
Рисунок 9 - Схема ИЛИ-НЕ

Для трех входных переменных получается таблица истинности с 2³ = 8 различными конфигурациями этих переменных. На выходе схемы всегда появляется 0, когда одна или большее число входных переменных равны 1. Нуль на выводе появляется в результате действия функции НЕ, которая инвертирует выходной сигнал. Таблица истинности различных состояний схемы И приведена в таблице 5.

Таблица 5

C B A	F
0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1

Из таблицы истинности следует, что F равна 1, если А, В и С равны 0, т. е. схема ведет себя для нулей на входе как функция И-НЕ. Для обозначения схемы НЕ используют символ в соответствии с рисунком 10. И здесь кружок на выходе схемы показывает, что функция НЕ входит в комбинацию ИЛИ-НЕ.

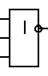
Рисунок 10 - Символы для схемы ИЛИ-НЕ

Выходной сигнал схемы ИЛИ-НЕ реализует функцию ИЛИ-НЕ для единиц на входе, т. е. на языке алгебры логики

_______

F = A + B + C,

или словами: F равна 0, если А или В или С или несколько этих переменных одновременно равны 1. Эта же схема реализует функцию НЕ-И для нулей на входе, поэтому можно записать

_ _ _

F = A*B*C,

или словами: F равна 1, если А и В и С равны 0.

______ _ _ _

При этом оказывается, что F = A+B+C = A*B*C, т. е. дополнение суммы переменных равно произведению их дополнений (теорема Де Моргана). Схема ИЛИ-НЕ реализует функцию ИЛИ-НЕ для единиц на входе и функцию И-НЕ реализует функцию для нулей на входе.

1.6. Аксиомы и законы булевой алгебры

Из таблиц истинности можно получить аксиомы и законы булевой алгебры. Из таблиц истинности для функций И, ИЛИ и НЕ можно получить аксиомы (тождества) для:

- функции И (0*0 = 0; 0*1 = 0; 1*0 = 0; 1*1 = 1);

- функции ИЛИ (0+0 = 0; 0+1 = 1; 1+0 = 1; 1+1 = 1);

_ _

- для функции НЕ (0 = 1; 1 = 0),

_ _

где 0 и 1 являются дополнениями для 0 и 1 соответственно.

Закон дуальности (теорема Де Моргана):

______ _ _ _

- A+B+C = A*B*C;

______ _ _ _

- A*B*C = A+B+C.

Ассоциативный закон: (А+В)+С = (А+С)+В; (A*B)*С = (A*C)*B.

Коммутативный закон: А+В = В+А; A*B = B*A.

Дистрибутивный закон: А*(В+С) = А*В+А*С; A+(B*C) = (A+B)*(A+C).

Закон поглощения: A+A*B = A; A*(A+B) = A.

2. Практическая часть

2.1. Изучить теоретическую часть лабораторно-практической работы.

2.2. Запустить на компьютере программу системы моделирования.

2.3. Провести исследования принципов работы элементарных логических схем.

2.4. Загрузить для исследования элементарной логической схемы И файл Л_И, для чего в верхней части экрана выбрать курсором мыши иконку «Загрузить схему из файла на диске», из списка файлов выбрать для исследования с названием Л_И.

2.5. Загрузить на экран мультиметр, для чего в верхней части экрана выбрать курсором мыши иконку «Получить мультиметр», передвинуть мультиметр (навести курсор мышки на изображение мультиметра, нажать левую кнопку мышки и, удерживая её, перемещать мышку) в левый верхний угол под иконки меню для удобного наблюдения. Включить вольтметр в положение измерения постоянного напряжения на пределе 20 В, для чего навести курсор мышки на мультиметре на цифру 20 в диапазоне пределов V_ и нажать левую кнопку мышки при этом на табло мультиметра загораться цифры. Подключить мильтимер к схеме, для чего курсор мышки навести на изображение зажима синего цвета в правом нижнем углу мультиметра, изображение курсора измениться со стрелки на кисть руки, нажать левую клавишу мышки, и удерживая ее нажатой, переместить новое изображение курсора на точку соединения нижнего вывода резистора со схемой, отпустить кнопку, при этом в этой точке появится изображение синего зажима. Аналогично подключить второй красный зажим мультиметра к на точку соединения верхнего вывода резистора со схемой.

2.6. Загрузить на экран осциллограф, для чего в верхней части экрана выбрать курсором мыши иконку «Получить осциллограф», передвинуть осциллограф (навести курсор мышки на изображение осциллографа, нажать левую кнопку мышки и, удерживая её, перемещать мышку) в правый нижний угол экрана для удобного наблюдения. Подключить канал А осциллографа к тем же точкам, что и мультиметр, используя вышеизложенную методику. Установить для данного канала значение усиление равное 5 В/дел.

2.7. Провести анализ схемы, представленной на экране монитора, для чего воспользоваться методикой исследования схемы из теоретической части лабораторно-практической работы. Функцию выключателя (включить или выключить) выбирать из меню после наведения курсора на выключатель и нажатия правой клавишей мышки, а подтверждать функцию, после выбора, – нажатием левой клавишей мышки.

2.8. На экране монитора будут наглядно представлены принцип работы элементарной логической схемы на мультиметре и вольтметре. Причем если F = 0, то мультиметр в цифровом виде, а осциллограф графически, будут отображать 0. Если же F = 1, то мультиметр в цифровом виде, а осциллограф графически, будут отображать 1.

2.9. Зарисовать данную элементарную логическую схему, к себе в тетрадь (допускается использовать схему из теоретической части работы, добавив условно изображение осциллографа).

2.10. Записать данные в тетрадь, используя форму таблицы (добавив дополнительный столбец для показаний мультиметра) соответствующей схемы из теоретической части лабораторно-практической работы.

2.11. Выйти из режима анализа схемы, для чего в верхней части экрана выбрать курсором мыши иконку «Нажатием этой кнопки можно очистить монтажную плату».

2.12. Загрузить для исследования элементарной логической схемы ИЛИ файл Л_ИЛИ, для чего в верхней части экрана выбрать курсором мыши иконку «Загрузить схему из файла на диске», из списка файлов выбрать для исследования с названием Л_ИЛИ. Причем при загрузке схемы мультиметр и осциллограф подключатся автоматически.

2.13. Повторить пункты 2.7., 2.8., 2.9, 2.10, 2.11.

2.14. Аналогично исследованию элементарной логической схемы ИЛИ из файла Л_ИЛИ проведите исследование элементарных логических схем НЕ, И-НЕ, ИЛИ-НЕ, загружая соответственно файлы Л_НЕ, Л_И_НЕ и Л_ИЛИ_НЕ соответственно.

2.15. Выйти из программы, для чего в верхней части экрана выбрать курсором мыши иконку «Выход».

2.16. На основании анализа каждой заполненной таблицы истинности с показаниями мультиметра сделать вывод о полной реализации каждой элементарной логической схемой соответствующей логической функции.

3. Контрольные вопросы

3.1. Какое выражение записано верно для ассоциативного закона?

3.1.1. (А+В)+С = (А+С)+В; (A*B)*С = (A*C)*B.

3.1.2. А+В = В+А; A*B = B*A.

3.1.3. А*(В+С) = А*В+А*С; A+(B*C) = (A+B)*(A+C).

3.1.4. A+A*B = A; A*(A+B) = A.

3.1.5. F = A+B+C = B*C.

3.2. Какое выражение записано верно для дистрибутивного закона?

3.2.1. (А+В)+С = (А+С)+В; (A*B)*С = (A*C)*B.

3.2.2. А+В = В+А; A*B = B*A.

3.2.3. А*(В+С) = А*В+А*С; A+(B*C) = (A+B)*(A+C).

3.2.4. A+A*B = A; A*(A+B) = A.

3.2.5. F = A+B+C = B*C.

3.3. Какое выражение записано верно для коммутативного закона?

3.3.1. (А+В)+С = (А+С)+В; (A*B)*С = (A*C)*B.

3.3.2. А+В = В+А; A*B = B*A.

3.3.3. А*(В+С) = А*В+А*С; A+(B*C) = (A+B)*(A+C).

3.3.4. A+A*B = A; A*(A+B) = A.

3.3.5. F = A+B+C = B*C.

3.4. Какое выражение записано верно для закона поглащения?

3.4.1. (А+В)+С = (А+С)+В; (A*B)*С = (A*C)*B.

3.4.2. А+В = В+А; A*B = B*A.

3.4.3. А*(В+С) = А*В+А*С; A+(B*C) = (A+B)*(A+C).

3.4.4. A+A*B = A; A*(A+B) = A.

3.4.5. F = A+B+C = B*C.

3.5. Как называется табличная запись состояний схемы И (ИЛИ, НЕ, И-НЕ, ИЛИ-НЕ)?

3.5.1. Таблица распределения.

3.5.2. Функция распределения.

3.5.3. Функция истинности.

3.5.4. Таблица истинности.

3.5.5. Таблица вероятностей.

3.6. Какое выражение записано верно для схемы И?

3.6.1. F = A*B*C = A\/B\/C.

3.6.2. F = AxBxC = A*B*C = A/\B/\C = A&B&C = ABC.

3.6.3. F = A+B+C = A&B&C.

3.6.4. F = AхBxC = A*B*C = A\/B\/C = A&B&C=ABC.

3.6.5. F = A+B+C = A/\B/\C.

3.7. Какое выражение записано верно для схемы ИЛИ?

3.7.1. F = A+B+C = A&B&C.

3.7.2. F = A+B+C = A/\B/\C.

3.7.3. F = A+B+C = A\/B\/C.

3.7.4. F = AхBxC = A*B*C = A\/B\/C = A&B&C = ABC.

3.7.5. F = AxBxC = A*B*C = A/\B/\C = A&B&C = ABC.

3.8. Какое выражение записано верно для схемы И-НЕ?

3.8.1. F = A\/B\/C.

_ _ _

3.8.2. F = A+B+C.

______

3.8.3. F = A+B+C.

_ _ _

3.8.4. F = A*B*C.

______

3.8.5. F = AхBxC.

3.9. Какое выражение записано верно для схемы ИЛИ-НЕ?

3.9.1. F = A\/B\/C.

_ _ _

3.9.2. F = A+B+C.

______

3.9.3. F = A+B+C.

______

3.9.4. F = AхBxC.

_ _ _

3.9.5. F = A*B*C.

3.10. Какое выражение записано верно для закона дуальности?

3.10.1. F = A+B+C = A*B

3.10.2. F = A+B+C = A*B*C

______ _ _ _

3.10.3. F = A+B+C = A*B*C

3.10.4. F = A+B+C = A*C

3.10.5. F = A+B+C = B*C

4. Оформление отчёта

Отчет должен содержать полученные данные в результате выполнения практической части работы и ответы на контрольные вопросы.