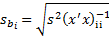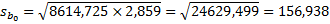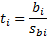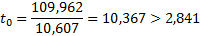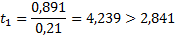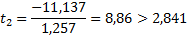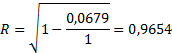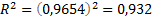- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
КАЗАХСКИЙ НАЦИОНАЛЬНЫЙ УНИВЕРСИТЕТ ИМ.АЛЬ-ФАРАБИ
КАЗАХСКИЙ НАЦИОНАЛЬНЫЙ УНИВЕРСИТЕТ ИМ.АЛЬ-ФАРАБИ

СРС
на тему
«Множественная линейная регрессия»
Подготовил: студент 3-го курса
группы «Учет и аудит», р/о
Муратбеков М.
Проверила: Кыстаубаева А.К.
Алматы 2020
СРС-2. Множественная линейная регрессия.
1.Предполагается, что объем предложения товара y линейно зависит от цены товара x1 и зарплаты сотрудников x2: 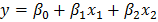 .
.
Статистические данные собраны за 10 месяцев.
| y | ||||||||||
| x1 | ||||||||||
| x2 |
1)Оценить по МНК коэффициенты уравнения регрессии.
2)Найти стандартную ошибку регрессии и стандартные ошибки коэффициентов регрессии.
3)Определить статистическую значимость коэффициентов теоретического уравнения линейной регрессии. Доверительная вероятность 99%.
4)Найти коэффициент детерминации и проверить гипотезу о его статистической значимости. Доверительная вероятность p=99%.
2.Дано уравнение линейной регрессии 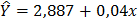 привести к показательному уравнению
привести к показательному уравнению 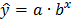 .
.
3.Дано уравнение линейной регрессии 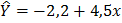 привести к степенному уравнению
привести к степенному уравнению 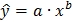 .
.
1.Предполагается, что объем предложения товара y линейно зависит от цены товара x1 и зарплаты сотрудников x2: 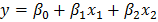 .
.
Статистические данные собраны за 10 месяцев.
| y | ||||||||||
| x1 | ||||||||||
| x2 |
1)Оценить по МНК коэффициенты уравнения регрессии.
2)Найти стандартную ошибку регрессии и стандартные ошибки коэффициентов регрессии.
3)Определить статистическую значимость коэффициентов теоретического уравнения линейной регрессии. Доверительная вероятность 99%.
4)Найти коэффициент детерминации и проверить гипотезу о его статистической значимости. Доверительная вероятность p=99%.
Решение:
1) Оценить по МНК коэффициенты уравнения регрессии.
S = (x’x)-1x’y
К матрице с переменными xj добавляем единичный столбец:
Матрица y
Матрица x’
Умножаем матрицы, (x’x)
| x’x = |
|
В матрице, (x’x) число 10, лежащее на пересечении 1-й строки и 1-го столбца, получено как сумма произведений элементов 1-й строки матрицы x’ и 1-го столбца матрицы x
Умножаем матрицы, (x’y)
| x’y = |
|
Находим обратную матрицу (x’x)-1
| (x’x) -1 = |
|
| y(x) = |
| * |
| = |
|
Уравнение регрессии:
y = 109.9623 + 0.8907x1-11.1366x2
2)Найти стандартную ошибку регрессии и стандартные ошибки коэффициентов регрессии.
| y | 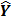
| e | e2 |
| 215,082 | 140,082 | 19622,967 | |
| 185,683 | 95,683 | 9155,275 | |
| 188,356 | 83,356 | 6948,106 | |
| 214,634 | 104,634 | 10948,232 | |
| 187,907 | 67,907 | 4611,374 | |
| 152,273 | 22,273 | 496,104 | |
| 167,864 | 37,864 | 1433,645 | |
| 192,361 | 62,361 | 3888,844 | |
| 161,180 | 26,180 | 685,413 | |
| 190,131 | 50,131 | 2513,117 | |
| 60303,078 |
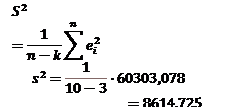 | ||||
| ||||
| ||||
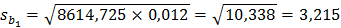
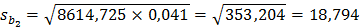
3)Определить статистическую значимость коэффициентов теоретического уравнения линейной регрессии. Доверительная вероятность 99%.
tтабл (n-m-1;α/2) = (7;0.025) = 2.841
|
|
Статистическая значимость коэффициента регрессии b0 подтверждается.
|
|
Статистическая значимость коэффициента регрессии b2 подтверждается.
Доверительный интервал для коэффициентов уравнения регрессии.
Определим доверительные интервалы коэффициентов регрессии (95%)
(bi - ti×Sbi; bi × ti*Sbi)
b0: (109,962 – 2,841×10,607 ; 109,962 + 2,841×10,607) = (79,829;140,096)
b1: (0,891 – 2,841×0,21 ; 0,891 + 2,841×0,21) = (0,294;1,488)
b2: (-11,137 – 2,841×1,257 ; -11,137 + 2,841×1,257) = (-14,708;-7,566)
4)Найти коэффициент детерминации и проверить гипотезу о его статистической значимости. Доверительная вероятность p=99%.
|
Коэффициент детерминации
|
H0: R2 = 0; β1 = β2 = ... = βm = 0.
H1: R2 ≠ 0.
Если F < Fkp = Fα ; n-m-1, то нет оснований для отклонения гипотезы H0.
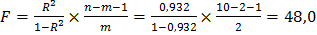 09
09
Табличное значение при степенях свободы k1 = 2 и k2 = n-m-1 = 10 - 2 - 1 = 7,
Fkp(2;7) = 4,74
Поскольку фактическое значение F > Fkp, то коэффициент детерминации статистически значим и уравнение регрессии статистически надежно.
2.Дано уравнение линейной регрессии 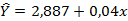 привести к показательному уравнению
привести к показательному уравнению 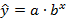 .
.
Решение:
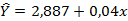
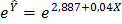
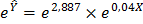
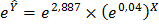 , привели к виду
, привели к виду 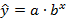
3.Дано уравнение линейной регрессии 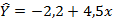 привести к степенному уравнению
привести к степенному уравнению 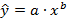 .
.
Решение:
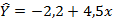
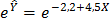
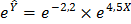
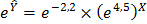 , привели к виду
, привели к виду 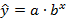
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|