
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
тогда получаем
Преобразование сумм тригонометрических функций в произведения Сегодня мы рассмотрим еще несколько тригонометрических формул, которые позволяют сумму (разность) синусов или косинусов разложить на множители. Эти формулы вам пригодятся при решении тригонометрических уравнений.
Первая формула - СУММА СИНУСОВ.
Рассмотрим выражение sin(s + t) + sin(s - t) , где s и t аргументы тригонометрических сункций.
Применим уже известные формулы синус суммы и синус разности:
sin(x + y) = sin x cos y + cos x sin y
sin(x - y) = sin xcos y - cos xsin y,
тогда выражение sin(s + t) будет иметь вид sin s cos t + coss sin t
а выражение sin(s - t) будет иметь вид sin s cos t - coss sin t,
тогда получим:
sin(s + t) + sin(s - t) = (sin s cos t + coss sin t) + (sin s cos t - coss sin t)
Раскрываем скобки:
sin s cos t + coss sin t+ sin s cos t - coss sin t
проводим вычисления:
coss sin t- coss sin t=0
sin s cos t + sin s cos t = 2 sin s cos t.
sin(s + t) + sin(s - t) = (sin s cos t + coss sin t) + (sin s cos t - coss sin t)=sin s cos t + coss sin t + sin scos t - cos ssin t =2 sin s cos t.
Таким образом получим, что выражение sin(s + t) + sin(s - t)= 2 sin s cos t.
Введем новые переменные х= s + t и у= s – t.
Сложим почленно эти равенства, то получим
х +у = s + t + s – t.
х +у = 2s
Найдем значение s
s = 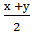 .
.
Во втором случае вычтем почленно эти равенства и получим
х -у = s + t - (s – t)
х -у = s + t - s + t
х - у = 2t
Найдем значение t
t = 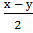 .
.
В выражении sin(s + t) + sin(s - t)= 2 sin s cos t
заменим s и t на введенные нами новые переменные:
s + t заменим на х
s – t заменим на у
s на 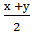
t на 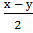 .
.
Тогда получим:
sinх + sinу= 2 sin 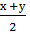 cos
cos 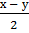
(сумма синусов двух аргументов равна удвоенному произведению синуса полусуммы этих аргументов на косинус их полуразности).
Пример.
sin 7х + sin3х =2 sin 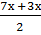 cos
cos 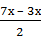 =2 sin 5х cos 2х.
=2 sin 5х cos 2х.
Вторая формула – РАЗНОСТЬ СИНУСОВ.
Для того, чтобы мы смогли применить уже выведенную формулу суммы синусов двух аргументов sinх + sinу= 2 sin 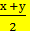 cos
cos 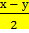
Воспользуемся тем, что синус – функция нечетная, т.е. - sin у = sin (- у),
sin х - sin у = sin х + sin(- у)
Теперь применим формулу суммы синусов, получим
=2 sin 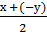 cos
cos 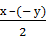 = 2 sin
= 2 sin 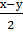 cos
cos 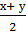 .
.
sin х - sin у = sin х + sin(- у) =2 sin 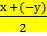 cos
cos 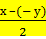 = 2 sin
= 2 sin 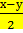 cos
cos 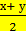 .
.
Следовательно, получили формулу разность синусов:
sin х - sin у =2 sin 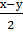 cos
cos 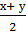 (разность синусов двух аргументов равна удвоенному произведению синуса полуразности этих аргументов на косинус их полусуммы).
(разность синусов двух аргументов равна удвоенному произведению синуса полуразности этих аргументов на косинус их полусуммы).
Пример. Упростить выражение sin 77° - sin 17°.
sin 77° - sin 17° =2 sin 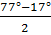 cos
cos 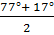 = 2 sin
= 2 sin 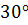 cos 47º.
cos 47º.
(так как sin 30º =  , то)= 2 ∙
, то)= 2 ∙  ∙ cos
∙ cos 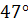 = cos
= cos 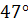 .
.
Третья формула – СУММА КОСИНУСОВ.
Для выражения cos (s + t) + cos (s - t) применим уже известные нам формулы косинус суммы и косинус разности:
cos (x + y) = cos x cos y - sin x sin y
cos (x - y) = cos xcos y + sin x sin y,
В выражение cos (s + t) + cos (s - t) подставим значения из формул и получим:
cos (s+ t)+ cos(s - t) = cos s cos t - sin s sin t + cos scos t + sin s sin t =2 cos s cos t
Значит cos (s+ t)+ cos(s - t) =2 cos s cos t
Введем новые переменные х= s + t и у= s – t. Как при выведении формулы СУММЫ СИНУСОВ.
s + t заменим на х
s – t заменим на у
s на 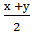
t на 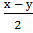 .
.
И получим формулу суммы косинусов
cos х+ cosу =2 cos 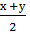 cos
cos 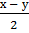
(сумма косинусов двух аргументов равна удвоенному произведению косинуса полусуммы этих аргументов на косинус их полуразности).
Пример. Упростить выражение cos (х+2у) + cos(3х - 2у).
cos (х+2у) + cos(3х - 2у) = 2 cos 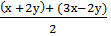 cos
cos 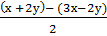 =
=
=2cos 2х cos( - х + 2у)= 2cos 2х cos( -( х - 2у)) ( а так как cos( - t) = cos t, то)=
= 2cos2х cos(х - 2у).
Четвертая формула – РАЗНОСТЬ КОСИНУСОВ.
Для выражения cos (s + t) - cos (s - t) применим уже известные нам формулы косинус суммы и косинус разности:
cos (x + y) = cos x cos y - sin x sin y
cos (x - y) = cos xcos y + sin x sin y, получим
cos (s+ t) - cos(s - t) = cos s cos t - sin s sin t- cos scos t - sin s sin t = - 2sin s sin t. Введем новые переменные х= s + t и у= s – t, значит, s = 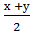 и t =
и t = 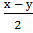 . Подставив введенные обозначения в формулу:
. Подставив введенные обозначения в формулу:
cos (s+ t) - cos(s - t) = - 2sin s sin t, получим формулу разность косинусов:
cos х – cos у = –2sin 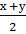 sin
sin 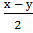 (разность косинусов двух аргументов равна взятому со знаком «минус» удвоенному произведению синуса полусуммы этих аргументов на синус их полуразности).
(разность косинусов двух аргументов равна взятому со знаком «минус» удвоенному произведению синуса полусуммы этих аргументов на синус их полуразности).
Пример. Упростить выражение cos 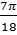 – cos
– cos  .
.
cos 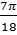 – cos
– cos  = - 2sin
= - 2sin 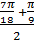 sin
sin 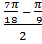 = - 2 sin
= - 2 sin  sin
sin 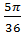 ( так как sin
( так как sin  =
= 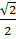 , то)=
, то)=
= - 2 ∙ 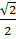 ∙ sin
∙ sin 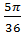 = -
= -  sin
sin 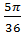 .
.
ПРИМЕР 1. Решить уравнение cos 6х + cos2х =0.
Решение. Преобразовав сумму косинусов в произведение по формуле:
(cos х + cosу = 2 cos 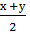 cos
cos 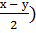 ,
,
2 cos 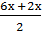 cos
cos 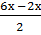 =0.
=0.
2 cos 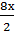 cos
cos 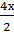 =0.
=0.
получим 2cos 4х cos2х = 0. Это уравнение обращается в верное равенство, если
cos 4х=0, или cos2х =0,
4х=  + πn,
+ πn, 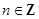 2х=
2х=  + πn,
+ πn, 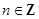
х=  +
+ 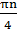 ,
, 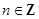 х=
х=  +
+ 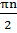 .
. 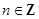
Ответ: х=  +
+ 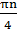 , х=
, х=  +
+ 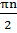 .
. 
ПРИМЕР 2. Решить уравнение sin7х + sin3х – sin5х =0.
Решение. Для суммы первого и второго слагаемых применим формулу сумма синусов
sin(x + y) = sin x cos y + cos x sin y
имеем:
(sin7х + sin3х) – sin5х =0
2 sin 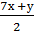 cos
cos 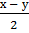 – sin5х =0
– sin5х =0
2 sin 5х cos 2х - sin5х =0.
Далее вынесем за скобку общий множитель sin5х и получим:
sin5х(2 cos 2х – 1) = 0.
sin5х = 0 или 2 cos 2х – 1 = 0,
Решений уравнения sin t = a принята для а=0:
sin t = 0 при t = πk,
тогда получаем
sin5х = 0
5х =πn, 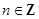
х = 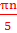 ,
, 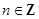 ( пи эн, деленное на пять)
( пи эн, деленное на пять)
Используя Табличные значения косинуса и определениерешения уравнения cos t = a, где (| а | 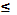 1) записывая в общем виде:
1) записывая в общем виде:
t = 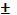 arccos а + 2πk
arccos а + 2πk
второе уравнение cos 2х=  имеет следующие решения
имеет следующие решения
Таблица
| аrсcos а | t | 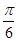
| 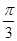
| 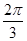
| 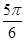
| 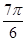
| 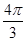
| 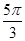
| 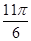
|
| а | cos t | 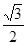
| 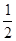
| 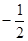
| 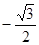
| 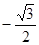
| 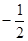
| 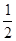
| 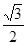
|
cos 2х=  .
.
2х= 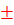 arccos
arccos  + 2πn,
+ 2πn, 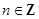
2х= 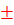
 + 2πn,
+ 2πn, 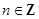
х = = 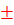
 + πn,
+ πn, 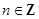
( плюс минус пи на шесть плюс пи эн).
Ответ: х = 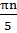 , х =
, х = 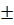
 + πn,
+ πn, 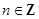
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|