
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Метод непосредственного интегрирования
Метод непосредственного интегрирования
Основной метод вычисления первообразной функции – это непосредственное интегрирование. Это действие основано на свойствах неопределенного интеграла, и для вычислений нам понадобится таблица первообразных. Прочие методы могут лишь помочь привести исходный интеграл к табличному виду.
Метод интегрирования, при котором интеграл с помощью тождественных преобразований подынтегральной функции и применения свойств интеграла приводится к одному или нескольким табличным интегралам, называется непосредственным интегрированием.
Таким образом, алгоритм действий следующий:
1. тождественное преобразование подынтегральной функции;
2. применение свойств неопределенного интеграла: вынесение константы за знак интеграла, представление интеграла от суммы функций в вид суммы интегралов;
3. использование таблицы интегралов.
В простейших примерах для применения непосредственного интегрирования достаточно разложить подынтегральную функцию на слагаемые и постоянные величины вынести за знак интеграла.
При определенной практике интегрирования обычно эти действия проводят устно, записывая лишь результат интегрирования.
Пример 1. Найти 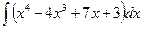 .
.
Решение. Представляя интеграл от алгебраической суммы в виде суммы интегралов слагаемых, вынося постоянные множители за знаки интегралов и применяя формулы 1, 2 таблицы основных интегралов, получим
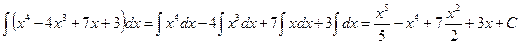 .
.
Замечание. Нет необходимости ставить произвольную постоянную после вычисления каждого интеграла, т.к. их сумма есть также произвольная постоянная, которую обозначают одной буквой и записывают в окончательный ответ.
Пример 2.Найти 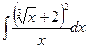 .
.
Решение. Возведём двучлен в квадрат и запишем каждое слагаемое в виде степенной функции, затем, произведя почленное деление и применив формулы 2, 3 таблицы основных интегралов, получим
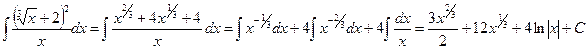 .
.
Пример 3. Найти 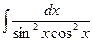 .
.
Решение. Заменив единицу в числителе выражением sin²x+cos²x и почленно разделив числитель на знаменатель, получим
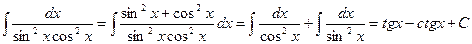 .
.
Пример 4.Найти 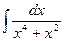 .
.
Решение. Прибавим и вычтем х² в числителе подынтегральной функции, вынесем за скобки х2 в знаменателе и почленно разделим числитель на знаменатель. Получим:
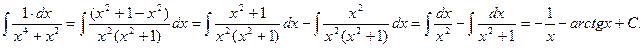
Пример 5.Найти .
Решение. Воспользуемся формулой тригонометрии 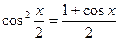 . Тогда получим
. Тогда получим
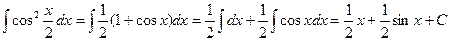 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|