Лекции 15, 16

04. 2.0 Физическая термодинамика - 6 часов

Лекции 15, 16

Статистическое описание равновесных состояний термодинамических систем: одно -, дву – и трехмерные функции распределения. Статистическое описание равновесных состояний термодинамических систем: определение средних значений случайных величин. Распределение Больцмана для идеального газа в однородном гравитационном поле: зависимость давления, концентрации и потенциальной энергии молекул от высоты. Распределение Больцмана для частиц, находящихся в поле центробежных сил. Принцип детального равновесия в системах, находящихся в состоянии термодинамического равновесия. Распределение Максвелла по абсолютным значениям скоростей: наиболее вероятная и средняя скорости молекул идеального газа. Функция распределения по значениям кинетической энергии поступательного движения молекул идеального газа. Экспериментальная проверка распределения Максвелла по абсолютным значениям скоростей молекул газа (опыт Ламмерта). Статистическое описание равновесного состояния термодинамических систем с помощью фазового пространства (каноническое распределение Гиббса). Распределение молекул идеального газа по координатам и скоростям (распределение Максвелла – Больцмана). Статистическое обоснование второго начала термодинамики: формула Больцмана для статистической энтропии. Явления переноса в газах. Термодинамические потоки: определение и классификация. Тепловой поток: уравнение и коэффициент теплопроводности. Поток импульса: уравнение и коэффициент вязкости. Диффузионный поток: уравнение и коэффициент диффузии. Эффузия в разреженном газе. Условие равновесия для разреженного газа. Физический вакуум. Броуновское движение. Производство энтропии в необратимых термодинамических процессах.

Статистическое описание равновесных состояний термодинамических систем: одно -, дву – и трехмерные функции распределения

Пусть xпараметр, определяющий состояние макроскопической системы, принимает

k дискретных значений: x₁, x₂, …, x_i, …, x_k. Значение x₁ наблюдалось при N₁измерениях, x₂ значение наблюдалось при N₂измерениях, …., x_i значение наблюдалось при N_i измерениях и последнее x_k значение этого параметра наблюдалось при N_k измерениях. Таким образом величина k - это количествогрупп измерений. В каждой из этих групп x параметр имеет дискретноеx_i значение, где

i = 1,2,3,…,k. Сумма N всех измерений c учётом k групп имеет следующий вид: N = ∑ N_i, (4.274)

i = 1

где i - номер группы измерений (i = 1,2,3,…,k), N_i - количество измерений, при которых параметримел

x_i значение. Увеличение числа проведённых экспериментовдо бесконечностиприводит к стремлению N_i/N отношения к следующему пределу: P(x_i) = lim N_i/N, (4. 275)

N→∞

где P (x_i) - вероятностьсобытия, что измеряемый x параметр будет иметь x_i значение. Вероятность P(x_i) представляет собой величину, которая может принимать значения в 0 ≤P (x_i) ≤ 1интервале. Значение P (x_i) = 0 соответствует случаю, когда ни при одном измерении не наблюдается x_i значение и, следовательно, система не может иметь состояние, характеризующееся x_i значением параметра.

Вероятность P(x_i) = 1 возможна только в том случае, если при всех измерениях наблюдалось лишь x_i значение. Тогда система находится в детерминированномсостоянии, характеризующимся x_i значением параметра.

В произвольный момент времени с P(x_i) вероятностью система находится в состоянии с x_i значением параметра. В следующий момент времени этот параметр может принять любое из k значений - x₁, x₂, …, x_i, …, x_k. При длительных и большом N количестве измерений x параметра его величина примет все x₁, x₂, …, x_i, …, x_k значения из ряда c соответствующими P(x₁), P(x₂), P(x₃),… P(x_i), … P(x_k)вероятностями.

Сумма P(x_i) вероятностейс учетом (4.260) имеет следующий вид:k k ∑ P(x_i) = (∑ N_i )/N = 1. (4. 276)

i = 1 i = 1; N→∞ Из выражения (4. 276) вероятностьпоявления события: параметр x имеет какое-либо x_i значение

в произвольный момент времени, есть событие достоверноеи вероятностьэтого события равна 1. Если x значения параметра могут принимать любое из значений в некотором a ≤ x ≤ b интервале, т.е. x значения параметра являются непрерывной величиной, то dP(x) вероятность попадания x значения этого параметра в интервал x…x + dx значений имеет следующий вид:

dP(x) = f(x)dx ↔ f(x) = dP(x)/dx, (4. 277) где f(x) - функция плотностивероятности, которая численноравна вероятности попадания значения

x параметра в единичный интервал измерений, например, вероятность нахождения P давления в интервале 100…101 Па значений P давления. Функция f(x) плотностивероятности не может быть отрицательнойвеличиной, т.е. для неё имеет место следующее неравенство: f(x) ≥ 0 (4. 278) и имеет размерность, обратнуюразмерности x параметра, например, если измеряется P давление в Па, то его f(P) - функция плотностивероятности давленияимеет размерность 1/Па. ВероятностьP(x₁≤ x ≤ x₂) попадания x значения измеренного параметра в x₁≤ x ≤ x₂интервал имеет следующий вид: x₂ P(x₁≤ x ≤ x₂) = ∫ f(x)dx, (4. 279) x₁

а весь a ≤ x ≤ b интервал возможных значений по аналогии с (4. 261), т.е. нахождениеизмеряемого

x параметра в интервалеего возможных значений есть достоверноесобытие и имеет следующий вид: b P(a ≤ x ≤ b) = ∫ f(x)dx = 1, (4. 280)

a Выражение (4. 280) называется условием нормировкиf(x) функции плотностивероятности.

Статистическое описание равновесных состояний термодинамических систем: определение средних значений случайных величин

Функция f(x) плотностивероятности позволяет определить < φ(x)> среднее значениеφ(x) функции, аргументомкоторой является измеряемый x параметр с a ≤ x ≤ b интервалом возможных значений, которое имеет следующее значение: b

< φ(x)> = ∫ φ(x) f(x)dx. (4. 281)

a Если состояние системы характеризуется двумя x, y или тремяx, y, z параметрами, то вероятноститого, что x, y значения находятся в x₁≤ x ≤ x₂, y₁≤ y ≤ y₂ интервалахили x, y, z находятся в интервалахx₁≤ x ≤ x₂, y₁≤ y ≤ y₂, z₁≤ z ≤ z₂ соответственно определяются из следующих выражений: x₂ y₂ x₂ y₂z₂

P(x₁≤ x ≤ x₂, y₁≤ y ≤ y₂) = ∫ ∫ f(x,y)dxdy; P(x₁≤ x ≤ x₂, y₁≤ y ≤ y₂, z₁≤ z ≤ z₂) = ∫ ∫ ∫ (x,y,z)dxdydz, (4. 282)

x₁y₁x₁y₁z₁

где f(x, y) и f(x, y, z) - соответственно двумернаяи трехмернаяфункции плотностивероятности. Примером двумерной f(x, y) функции плотностивероятности может служить совместнаяфункция для координат и скоростей молекул газа. ВероятностьdP(x,y) одновременного попадания x значения параметра в x…x + dx интервал, а значения y параметра в y…y + dy интервал по аналогии с одномерным случаем (4.262) имеет следующий вид: dP(x,y) = f(x,y) dxdy. (4. 283) В случае статистическойнезависимости x и y значений параметровмежду собой двумерная функция плотностивероятности f(x, y) этих параметров равна произведениюодномерных функций f(x) и f(y) плотностивероятностикаждогоx и y параметра, вследствие чего имеет место следующее выражение: f(x, y) = f(x)f(y). (4. 284)

Распределение Больцмана для идеального газа в однородном гравитационном поле: зависимость давления, концентрации и потенциальной энергии молекул от высоты

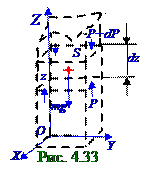
Атмосферное P давление Земли (рис. 4.33) при замене воздуха идеальным газом зависит от z высоты. На z+dz высоте (рис. 4.33) оно равно P+dP, а на z высоте оно равно P, поэтому элементарное приращение dP давления этого идеального газа определяется из равновесия области идеального газа dz высотой и S площадью поверхности. Второй законНьютонавИСО (1.42) из раздела 1.0 "Физические основы механики" (рис. 4.33) для области идеального газа dz высотой, S площадью поверхности и m массой, к которой сверху приложено P+dP давление, а снизу действует P давление, в проекции : :

на OZ ось имеет следующий вид:

OZ: 0 = - mg - (P+dP)S + PS ↔ 0 = - ρdzSg - (P+dP)S + PS ↔ dP =- ρgdz, (4. 285)

где ρ - плотностьидеального газа в элементарной области dV = Sdz объёмом.

Уравнение (4.13) из раздела 4.1 "Физическая термодинамика"Клапейрона - Менделееваотносительно ρ плотности идеального газа имеет следующий вид:

PV = (M/μ)RT ↔ M/V = (Pμ)/RT ↔ ρ = (Pμ)/RT, (4. 286) где T - температуры идеального газа; ρ = M/V - плотностьидеального газа; M, V - соответственно масса, объём идеального газа.

Подставляем (4.286) в (4.285) и получаем следующее выражение P давления воздуха в зависимости от zрасстояния до поверхности Земли:

dP/P = - (μg/RT)dz ↔ ∫ dP/P = - ∫(μg/RT)dz ↔ lnP = -(μgz /RT) + lnc↔ P = cexp(-μgz /RT). (4. 287) При z = 0 постоянная c интегрирования имеет следующий вид: c = P₀, (4. 288) т.е. эта c постоянная интегрирования равна P₀ атмосферному давлению воздуха на поверхности Земли, который при выводе (4. 287) выражения принят идеальным газом.

Подставим (4. 288) в (4. 287) и получим следующее распределение Больцманадля P давления идеального газа в однородном гравитационном поле: P = P₀exp(-μgz/RT). (4. 289)

С учётом (4.31) из раздела 4.1 "Физическая термодинамика" основного P = nkTуравнения молекулярно - кинетической теории выражение (4.289) примет следующий вид распределения Больцмана для n концентрации идеального газа в однородном гравитационном поле: n = n₀ exp(-m_igz/kT), (4. 290) где n₀ - концентрация молекул идеального газа на поверхности Земли, m_i - масса молекулы,

k - постоянная Больцмана.

РаспределениеБольцмана молекул идеального газа в однородном гравитационном поле Земли по высоте устанавливается в результате:

1. притяжения молекул к Земле под влиянием их вектора m_ig силы тяжести, которое стремится расположить их на поверхности Земли;

2. тепловогодвижения, характеризуемого T температурой, которое стремится разбросать молекулы равномерноповсей z высоте от Земли.

Чем больше m_i масса молекул и меньше T температура идеального газа, тем сильнее преобладает перваятенденция, и молекулы сгущаются у поверхности Земли. В пределе при стремлении T температуры идеального газа к нулю, т.е.T → 0, тепловоедвижение молекул идеального газа совсем прекращается и под влиянием притяжениямолекулы располагаются на земной поверхности. На разной z высотемолекулы m_i массой обладают различным запасом (1.105) из раздела 1.0 "Физические основы механики"потенциальной энергии, величина которой имеет следующий вид: W_pi = m_igz. (4. 291) Подставляем (4. 291) в (4. 290) и получаем следующее выражение nконцентрации молекул воздуха в зависимости от W_piпотенциальной энергии этих молекул в гравитационном поле Земли: n = n₀exp(-W_pi/kT), (4. 292) где n - концентрациямолекул в том месте пространства, где отрицательная потенциальная энергия притяжения молекул к Землеимеет значение "-W_pi"; n₀ - концентрациямолекул в том месте пространства, где отрицательная "-W_pi" потенциальная энергия притяжения этих молекул к Земле имеет значение, равное нулю, т.е.на поверхности Земли.

Согласно (4.292) распределению Больцмана в любом потенциальномполе сил n концентрация молекул распределяется в соответствии с их W_piпотенциальной энергией в этом поле. Чем больше отрицательная"-W_pi"потенциальная энергия притяжения молекул, т.е. чем ближе молекулы к поверхности Земли, тем согласно (4.292) больше n концентрация молекул.

Распределение Больцмана для частиц, находящихся в поле центробежных сил

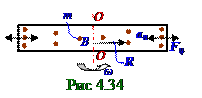
На частицы (рис. 4.32) m массой, находящихся во вращающемся с (1.19)из раздела 1.0. "Физические основы механики" ω угловойскоростьювокруг неподвижной OO оси,цилиндрическом сосуде и вектором (1.26) из раздела 1.0 "Физические основы механики" a_n нормального ускорения действует вектор F_ц инерциальной или центробежной силы. Этот вектор F_ц центробежной силы

коллинеарен (1.26) из раздела 1.0 "Физические основы механики" вектору a_n нормального ускорения, с которым эта частица m массой двигается по окружности R радиуса, и направлен в противоположную сторону относительно этого вектора a_n нормального ускорения.

Проекция F_ц_R вектора F_ц центробежной силы (рис. 4.34) на направление вектора (рис.1.10) из раздела 1.0 "Физические основы механики" R радиуса, проведённого из центра B окружности, по которой движется частица m массой, в эту частицу, с учётом модуля a_n вектора a_n нормального ускорения (1.26) из раздела 1.0 "Физические основы механики" имеет следующий вид: F_ц_R = ma_n= mω²R, (4. 293)

где положительное значение проекции F_и_R вектора F_и центробежной силы в (4. 293) выражении потому, что вектор F_ц центробежной силы коллинеарен вектору R радиуса и направлен с ним в одну сторону.

Проекция F_ц_R вектора F_ц центробежной силы, действующей на частицу m массой, в произвольной точкеполя центробежных сил на направление вектора dRэлементарного перемещения по (рис. 4.34) вектору R радиуса согласно (1.98) из раздела 1.0 "Физические основы механики" равна с противоположнымзнаком dW_p_ц/dR производной W_p_цпотенциальной энергии в этой точкеполя центробежных сил, вследствие чего с учётом (4. 293) проекция F_ц_R вектора F_ц центробежной силы имеет следующий вид: R

F_ц_R = - dW _p_ц/dR ↔ dW _p_ц= - mω²RdR ↔ W _p_ц= - mω²∫RdR = - mω²R²/2, (4. 294)

где dW_p_ц/dRпроизводнаяW_p_цпотенциальной энергии по R радиусу окружности, по которой движется частица m_i массой не частная потому, что вектор F_ц центробежной силы в произвольной точкеполя центробежных сил коллинеарен вектору R радиуса, т.е. проекции этого вектора F_ц центробежной силы на другие направления отсутствуют.

Подставляем (4. 294) выражение потенциальнойW_p_цэнергиичастицы m массой в поле центробежных сил в выражение (4. 292) распределения Больцманаи получаем следующее выражение

nконцентрацииэтих частиц в поле центробежных сил в зависимости от квадрата ω² угловойскорости вращения цилиндрического сосуда (рис 4.34) вокруг неподвижной OO оси и квадрата R² радиуса, проведённого из B центра окружности, по которой движется частица m массой: n = n₀ exp(- W_p_ц/kT) = n₀exp(mω²R²/2kT), (4. 295)

где n₀ - концентрациячастиц m массой на неподвижной OO оси, т.е. при значении Rрадиуса, проведённого из B центра окружности, по которой движется частица m массой, равного нулю, т.е. при R = 0.

Принцип детального равновесия в системах, находящихся в состоянии термодинамического равновесия

Статистическое описание равновесных состояний термодинамических систем можно выполнить, предполагая, что в термодинамической системе, находящейся в состоянии термодинамического равновесия, два любых противоположно направленных процесса взаимно скомпенсированы.

Требование взаимной компенсациидвух любых противоположно направленных процесса выражается в следующем принципедетального равновесия: в равновесной термодинамической системе вероятности протекания прямого и обратногопроцессов одинаковы. Под обратнымпонимают процесс, который полностью совпадает с прямым при замене течениявремени на противоположное. Например, если прямойпроцесс заключается в соударениидвух шаров, при котором их векторы v₁, v₂начальныхскоростей становятся равными векторам v'₁, v'₂скоростей, то выполнение принципадетального равновесиябудет заключаться в том, что при соударениитех же шаров с векторами

v'₁, v'₂начальныхскоростей их векторы скоростей становятся равными v₁, v₂.

Пространство скоростей молекул идеального газа, находящегося в состоянии термодинамического равновесия

Возьмём в воображаемом пространстве, которое называется v - пространством или пространством скоростей, прямоугольную декартову (рис. 1.1) из раздела 1.0 "Физические основы механики"систему координат, по координатным Ov_X, Ov_Y и Ov_Z осям которой будем откладывать (рис. 4. 35) проекции v_iX_,v_iY и v_iZ вектораv_iскорости молекул.

Число dN молекул, проекции v_iX_,v_iY и v_iZ на Ov_X, Ov_Y и Ov_Z оси вектораv_i скорости i-ой молекулы которых лежат в интервале значений v_X…v_X + dv_X, v_Y … v_Y + dv_Y и v_Z… v_Z + dv_Z, т.е. в

(рис. 4. 33) элементарном прямоугольном dV = dv_Xdv_Y dv_Z объёме скоростей, расположенного по направлению этого вектора v_i скоростей молекул, имеет следующее значение:

dN = Nf(v)dv_Xdv_Ydv_Z= Nf(v)dV, (4. 296) где N - полное число молекул в данной массе газа, в которой измеряются скоростимолекул; f(v) - функция плотности вероятности, численно равная (4. 277) вероятности нахождения v_i модуля вектораv_i скоростей молекул в единичном прямоугольном объёме по направлению этого вектора

v_i скоростей молекул; Nf(v) - количество (рис. 4.35) молекул из полного N числа молекул в данной массе газа, находящихся в единичном прямоугольном Vобъёме по направлению вектора v_i скоростей молекул.

Модули v_i вектора v_i скоростей молекул, значения которых находятся в пределах (рис. 4. 35) от v до v + dv попадают в область, лежащую между сферами v и v+dvрадиусов. Объём dV_vэлементарного шарового слоя с учетом S площади сферы vрадиусоми его dv толщины имеет следующее значение: dV_v = 4πv²dv. (4. 297) Число dN_v молекул, имеющих v_i модули векторов v_i скоростей в интервале от v до v + dv, т.е. попадающие в (4. 297) элементарный шаровой слой dV_v объёмом, с учетом (4. 296) f(v) функции плотности, которая численно равна вероятности нахождения v_i модуля вектораv_i скоростей молекул в единичном прямоугольном объёме по направлению этого вектора v_i скоростей молекул, имеет следующее значение: dN_v= N f(v)dV_v = N f(v)4πv²dv = NF(v)dv, (4. 298) где F(v) - функция плотности вероятности, численно равная

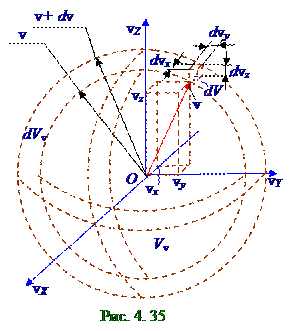
(рис. 4. 35) вероятности нахождения v_i модулей вектораv_i скоростей молекул в шаровомслое с внутренним радиусом, равным этому модулю v_i вектораv_i скоростей молекул, и толщиной, равной единичному интервалу, например, находящихся в интервале модулей v_i вектораv_i скоростей молекул 500…501 м/с, по всемвозможным направлениямэтих векторовv_i скоростей молекул.

Разделив (4. 298) число dN_v молекул, на N полное число молекул в данной массе газа, получим (4. 277) вероятность dP_v нахождения модулей v_i вектораv_i скоростей молекул в элементарном шаровом

(рис. 4. 35) слое dV_v объёмом с внутренним и внешнимирадиусами соответственно v; v + dv, имеющей следующий вид: dN_v/N = dP_v = f(v)4πv²dv = F(v)dv, (4. 299) где dN_v- число молекул, имеющих модули v_i вектораv_i скоростей в интервале от v до v + dv, т.е. попадающие (рис. 4. 35) в элементарный шаровой слой dV_v объёмом; N - полное число молекул в данной массе газа, в которой измеряются скоростимолекул.

Распределение Максвелла по абсолютным значениям скоростей: наиболее вероятная и средняя скорости молекул идеального газа

Вероятность (4. 277) dP_Xтого, что проекция v_iX (рис. 4. 35) на Ov_X ось вектораv_i скоростей молекул находится в интервале от v_X до v_X + dv_X, может быть по аналогии с (4. 284) представлена в следующем виде: dN_vX /N = dP_vX = f(v_X)dv_X, (4.300) где f(v_X) - функция плотностивероятности, которая численноравна вероятности нахождения проекций v_iX на Ov_X ось вектораv_i скоростей молекул в единичном интервале, например, находящихся в интервале 500…501 м/с этих v_iX проекций на Ov_X ось вектораv_i скоростей молекул; dN_vX - число молекул, имеющих проекции v_iX на Ov_X ось векторов скоростей молекул в интервале от v_X до v_X + dv_X; N - полное число молекул в данной массе газа, в которой измеряются скоростимолекул. Аналогичные (4.300) dP_vY, dP_vZ вероятности для двух других проекций v_iY и v_iZ на Ov_Y и Ov_Z оси вектораv_i скоростей молекул соответственно с учётом (4. 243) имеют следующий вид: dP_vY = f(v_Y)dv_Y; dP_vZ = f(v_Z)dv_Z. (4.301) В силу равноправности всех направленийдвижения молекул аналитический вид f(v_X), f(v_Y) и f(v_Z) функций плотностивероятности из (4.300) и (4.301) одинаков. Вследствие статистическойнезависимости между собой проекций v_iX_,v_iY и v_iZ на

Ov_X, Ov_Y и Ov_Z оси вектораv_i скоростей молекултрёхмерная(4. 282) функция плотностивероятностиf(v_X, v_Y, v_Z) равна следующему произведению одномерных(4.300), (4.301) функций плотностейвероятности: f(v_X, v_Y, v_Z) = f(v_X) f(v_Y) f(v_Z). (4.302) Вероятность dP_vX_,_vY_,_vZ одновременного (4. 283) нахождения значений проекций проекций v_iX_,v_iY и v_iZ на Ov_X, Ov_Y и Ov_Z оси вектораv_i скоростей молекул, лежащих в интервалах

v_X…v_X + dv_X, v_Y…v_Y + dv_Y и v_Z…v_Z + dv_Z (рис. 4. 35) равняется произведению трёхмерной(4.302)

f(v_X, v_Y, v_Z) функции плотностивероятности на элементарный прямоугольный dV = dv_Xdv_Ydv_Z объём скоростей, расположенный по направлению этого вектора v_i скоростей молекул, вследствие чего эта dP_vX_,_vY_,_vZ вероятность имеет следующий вид: dP_vX_,_vY_,_vZ = f(v_X) f(v_Y) f(v_Z)dv_Xdv_Ydv_Z. (4.303) Разделим левуюи правую части (4. 304) на N - полное число молекул в данной массе газа и получим аналогично (4.299) вероятность dP_vX_,_vY_,_vZ одновременного (4. 267) нахождения значений проекций v_iX_,v_iY и v_iZ на Ov_X, Ov_Y и Ov_Z оси вектораv_i скорости молекул, лежащих (рис. 4. 35) в интервалах v_X…v_X + dv_X, v_Y…v_Y + dv_Y и v_Z…v_Z + dv_Z, которая имеет следующий вид:

dP_vX_,_vY_,_vZ = dN/N = f(v)dv_Xdv_Ydv_Z. (4.304) Приравниваем правые части (4.303) и (4.304), т.к. левые части этих выражений равны, и получаем следующее выражение: f(v) = f(v_X) f(v_Y) f(v_Z) ↔ lnf(v) = lnf(v_X) + lnf(v_Y) + lnf(v_Z). (4.305) Продифференцируем правую и левую части (4.305) выражения по переменной v_iX - проекции на Ov_X ось вектораv_i скоростей молекул, используя "цепное правило" дифференцирования сложной функции, вследствие чего имеет место следующее выражение: {∂[lnf(v)]/∂[f(v)]}[∂f(v)/∂v] (∂v/∂v_X) = = {∂[lnf(v_X)]/∂[f(v_X)]}[∂f(v_X)/∂v_X](∂v_X/∂v_X) ↔ [1/f(v)][∂f(v)/∂v](∂v/∂v_X) = [1/f(v_X)][∂f(v_X)/∂v_X]. (4.306) Поскольку v_i модуль вектораv_iскоростей молекул (1.10) из раздела 1.0 «Физические основы механики» имеет вид: v_i = (v_iX²+ v_iY² + v_iZ²)^1/2, то частная производнаяот этого v_i модуля по переменной величине проекции v_iX на Ov_X ось вектораv_i скоростей молекул в (4.250) имеет следующий вид: ∂v/∂v_X = v_X /(v_X²+ v_Y ²+ v_Z ²)^1/2 = v_X/v. (4.307) Подставляем (4.307) в (4.306), а также подставляем (4.302) f(v) = f(v_X) f(v_Y) f(v_Z) - функцию плотности вероятности, численноравнуювероятностиодновременного (4. 284) нахождениязначений

проекций v_iX_,v_iY и v_iZ на Ov_X, Ov_Y и Ov_Z оси вектораv_i скорости молекул (рис. 4.35) в единичном интервале значений, тоже в (4.306), вследствие чего получаем следующее выражение:

[1/f(v)][∂f(v)/∂v]/v =[1/f(v_X)][∂f(v_X)/∂v_X]/v_X ↔ [1/f(v_X) f(v_Y) f(v_Z)][∂f(v)/∂v]/(v_X²+ v_Y ²+ v_Z ²)^1/2 =