
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Наибольшее и наименьшее значения функции на отрезке
Наибольшее и наименьшее значения функции на отрезке
Функция 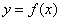 непрерывна на отрезке
непрерывна на отрезке 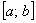 если:
если:
1) она непрерывна на интервале 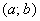 ;
;
2) непрерывна в точке 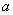 справа и в точке
справа и в точке 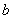 слева.
слева.
Функция 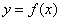 непрерывна в точке
непрерывна в точке 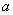 справа, если она определена в данной точке и её правосторонний предел совпадает со значением функции в данной точке:
справа, если она определена в данной точке и её правосторонний предел совпадает со значением функции в данной точке: 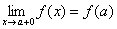 . Она же непрерывна в точке
. Она же непрерывна в точке 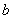 слева, если определена в данной точке и её левосторонний предел равен значению в этой точке:
слева, если определена в данной точке и её левосторонний предел равен значению в этой точке: 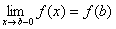
Представьте, что зелёные точки – это гвозди, на которых закреплена волшебная резинка:
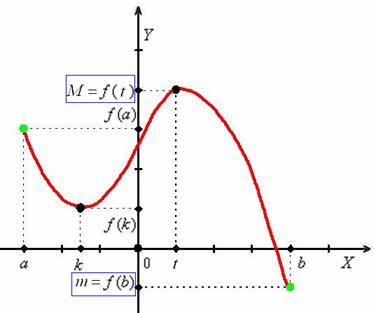
Мысленно возьмите красную линию в руки. Очевидно, что как бы далеко мы не растягивали график вверх и вниз (вдоль оси 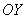 ), функция всё равно останется ограниченной – изгородь сверху, изгородь снизу, и наше изделие пасётся в загоне. Таким образом, непрерывная на отрезке функция ограничена на нём. В курсе матанализа этот вроде бы простой факт констатируется и строго доказывается первой теоремой Вейерштрасса
), функция всё равно останется ограниченной – изгородь сверху, изгородь снизу, и наше изделие пасётся в загоне. Таким образом, непрерывная на отрезке функция ограничена на нём. В курсе матанализа этот вроде бы простой факт констатируется и строго доказывается первой теоремой Вейерштрасса
Согласно второй теореме Вейерштрасса, непрерывная на отрезке 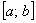 функция достигает своейточной верхней грани
функция достигает своейточной верхней грани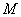 и своейточной нижней грани
и своейточной нижней грани 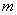 .
.
Число 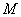 также называют максимальным значением функции на отрезке и обозначают через
также называют максимальным значением функции на отрезке и обозначают через 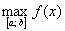 , а число
, а число 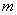 – минимальным значением функции на отрезке с пометкой
– минимальным значением функции на отрезке с пометкой  .
.
В нашем случае:
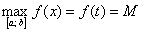
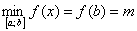
Грубо говоря, наибольшее значение находится там, где самая высокая точка графика, а наименьшее – где самая низкая точка.
Важно!наибольшее значение функции и наименьшее значение функции – НЕ ТО ЖЕ САМОЕ, что максимум функции и минимум функции. Так, в рассматриваемом примере число 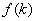 является минимумом функции, но не минимальным значением.
является минимумом функции, но не минимальным значением.
Алгоритм лежит на поверхности и напрашивается из приведённого рисунка:
1) Находим значения функции в критических точках, которые принадлежат данному отрезку.
2) Вычисляем значения функции на концах отрезка.
3) Среди найденных в 1-м и 2-м пунктах значений функции выбираем самое маленькое и самое большое число, записываем ответ.
Пример 1
Найти наибольшее и наименьшее значения функции 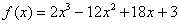 на отрезке
на отрезке 
Решение:
1) Вычислим значения функции в критических точках, принадлежащих данному отрезку:
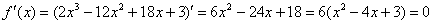
Полученное квадратное уравнение имеет два действительных корня:
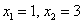 – критические точки.
– критические точки.
Первая критическая точка принадлежит данному отрезку: 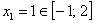
А вот вторая – нет: 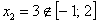 , поэтому про неё сразу забываем.
, поэтому про неё сразу забываем.
Вычислим значение функции в нужной точке:
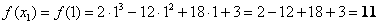
Итоговый результат я выделил жирным цветом, при оформлении задания в тетради его удобно обвести в кружок простым карандашом или пометить как-то по-другому.
2) Вычислим значения функции на концах отрезка:
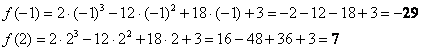
Результаты опять каким-либо образом выделяем.
3) выбираем наибольшее и наименьшее.
Ответ: 
Пример 2
Найти наибольшее и наименьшее значения функции 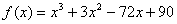 на отрезке
на отрезке 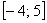
Это пример для самостоятельного решения. Примерный образец чистового оформления в конце
!Во-первых, критических точек может не оказаться вообще. Это очень хорошо – меньше вычислений. Просто записываем вывод: «критические точки отсутствуют» и переходим ко второму пункту алгоритма.
Во-вторых, все критические точки (одна, две или бОльшее количество) могут не принадлежать отрезку. Замечательно. Пишем следующее: «критические точки (а) не принадлежат (ит) рассматриваемому отрезку». Находить какие-то значения функции здесь, разумеется, тоже не надо.
Пример 3
Найти наибольшее и наименьшее значения функции на заданном отрезке
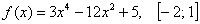
Решение: всё опять начинается дежурной фразой:
1) Вычислим значения функции в критических точках, принадлежащих данному отрезку:
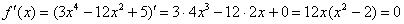
Да, критических точек тут и правда целая команда:
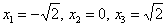
Первые две точки принадлежат нашему отрезку:

Но третья оказывается вне игры: 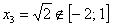
(надеюсь, все сумели сосчитать 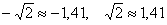 )
)
Вычислим значения функции в подходящих точках:
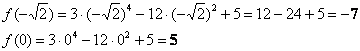
2) Вычислим значения функции на концах отрезка:
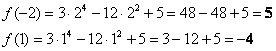
Ответ: 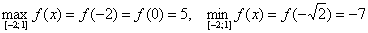
Время от времени критические точки могут совпадать с одним или даже с обоими концами отрезка, и в этом случае укорачивается второй этап решения. Следующий пример для самостоятельного изучения посвящен как раз такой ситуации:
Пример 4
Найти наибольшее и наименьшее значения функции на заданном отрезке
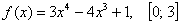
Примерный образец решения в конце урока.
Пример 5
Найти максимальное и минимальное значения функции на отрезке
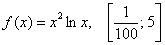
Решение: отрезок, надо сказать, творческий, но пример взят из конкретной контрольной работы и ни в коем случае не придуман.
1) Вычислим значения функции в критических точках, которые принадлежат данному отрезку:
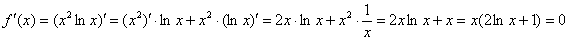
Очевидный корень оказывается не в теме: 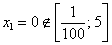 .
.
Решаем уравнение:
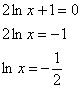
Второй корень принадлежит нашему отрезку: 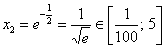
Вычислим значение функции во второй критической точке:
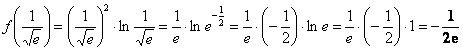
2) Вычислим значения функции на концах отрезка:

3) «Жирные» результаты получены с экспонентами и логарифмами, что существенно затрудняет их сравнение. По сей причине вооружимся калькулятором либо Экселем и вычислим приближённые значения, не забывая, что 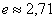 :
:
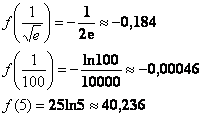
Вот теперь всё понятно.
Ответ: 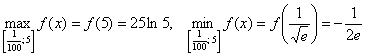
Дробно-рациональный экземпляр для самостоятельного решения:
Пример 6
Найти максимальное и минимальное значения функции на отрезке
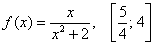
Вычисления в данном случае не менее кропотливы и точно так же потребуют вмешательства калькулятора (если вы, конечно, не вундеркинд). Полное решение и ответ в конце
Пример 7
Найти максимальное и минимальное значения функции на отрезке
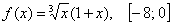
Решение:
1) Найдём критические точки. Предварительно можно раскрыть скобки, но не особо сложнее использовать и правило дифференцирования произведения:
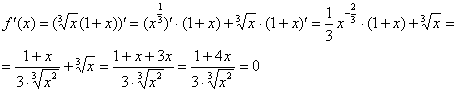
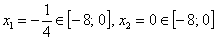 – критические точки.
– критические точки.
Обратите внимание, что точка 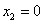 обращает знаменатель производной в ноль, но её следует отнести к критическим значениям, поскольку САМА ФУНКЦИЯ определена в данной точке.
обращает знаменатель производной в ноль, но её следует отнести к критическим значениям, поскольку САМА ФУНКЦИЯ определена в данной точке.
Кроме того, данная точка совпала с правым концом отрезка, а значит, в следующем пункте будет меньше расчётов. В следующем, но не сейчас:
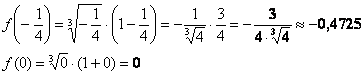
2) Вычислим значения функции на концах отрезка:
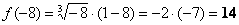
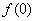 уже известно.
уже известно.
Ответ: 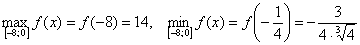
Решения и ответы:
Пример 2: Решение:
1) Вычислим значения функции в критических точках, принадлежащих данному отрезку:
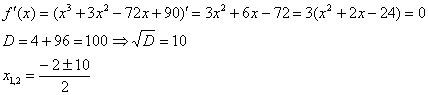
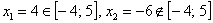 – критические точки.
– критические точки.
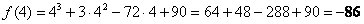
2)Вычислим значения функции на концах отрезка:
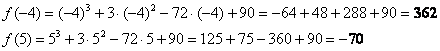
Ответ: 
Пример 4: Решение:
1) Вычислим значения функции в критических точках, принадлежащих данному отрезку:
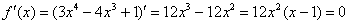
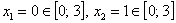 – критические точки.
– критические точки.

2) Вычислим значения функции на концах отрезка:
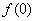 уже рассчитано в предыдущем пункте.
уже рассчитано в предыдущем пункте.
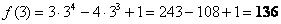
Ответ: 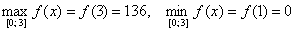
Пример 6: Решение:
1) Вычислим значения функции в критических точках, которые принадлежат данному отрезку:
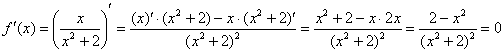
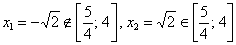 – критические точки.
– критические точки.
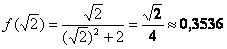
2) Вычислим значения функции на концах отрезка:
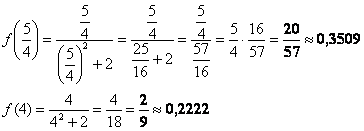
Ответ: 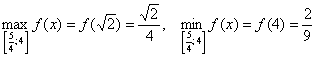
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|