Неравенство Маркова. Неравенство Чебышева

Неравенство Маркова. Неравенство Чебышева

Неравенство Маркова дает вероятностную оценку того, что значение неотрицательной случайной величины превзойдет некоторую константу через известное математическое ожидание. Когда никаких других данных о распределении нет, неравенство дает некоторую информацию, хотя зачастую оценка груба или тривиальна.

Пусть X - случайная величина, принимающая неотрицательные значения, M(X) - ее конечное математическое ожидание, то для любых a>0 выполняется

P(X ≥ a) ≤ M(X)/a. (1)

Альтернативная форма записи (когда нужно оценить вероятность того, что СВ меньше некоторой константы):

P(X < a)>1−M(X)/a. (2)

Когда известны не только математическое ожидание (первый момент), но и дисперсия (второй центральный момент) для случайной величины (и они конечны), можно применять следствие неравенства Маркова — неравенство Чебышева, которое дает оценку вида:

P(|X−M(X)| ≥ a) ≤ D(X)/a², a>0. (3)

Также его можно записать в другой форме:

P(|X−M(X)|<a)>1−D(X)/a², a>0. (4)

Неравенство Чёбышева показывает, что случайная величина принимает значения близкие к среднему (математическому ожиданию) и дает оценку вероятности больших отклонений.

Положим a=kσ, где σ - стандартное отклонение, тогда получим оценку вероятности того, что СВ отклонится по модулю от среднего больше чем на kσ:

P(|X−M(X)|≥kσ) ≤ 1/k². (5)

Для значения k=2 вероятность отклонения меньше 25%, для k=3 - уже 11,12%.

Для случайной величины X, распределенной по биномиальному закону с параметрами n,p неравенство Чебышева принимает вид:

P(|X−np|<a)>1−npq/a². (6)

Для частоты k/n появления события в n независимых испытаниях, в каждом из которых оно происходит с вероятностью p (дисперсия этой величины D(k/n)=pq/n) получаем:

P(k/n−p∣<a) >1−pqn/a². (7)

Последнее неравенство также можно получить из теоремы Бернулли. Из последнего неравенства также есть следствие, которое позволяет оценить отклонение числа 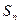появлений события в n испытаниях от ожидаемого значения np:

P(| 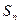−np|<a)>1−npq/a². (8)

Приведем также теорему Чебышева, которая имеет большое практические значение.

Если дисперсии n независимых случайных величин X1,X2,...,Xn ограничены одной и той же постоянной, то при неограниченном увеличении числа n средняя арифметическая случайных величин сходится по вероятности к средней арифметической их математических ожиданий a1,a2,...,an, т.е.

limn→∞P(∣X1+X2+...+Xn−a₁+a₂+...+an∣≤ε)=1. (9)

Следствие: Если независимые случайные величины X1,X2,...,Xn имеют одинаковые математические ожидания, равные a, а их дисперсии ограничены одной и то же постоянной C, то:

P(∣X1+X2+...+Xn−a∣≤ε)≥1−C/nε² (10)

Это означает, что при большом числе испытаний практически достоверно, что их средняя

арифметическая (случайная величина) как угодно мало отличается от неслучайной величины a (среднего значения). Это суть закона больших чисел.

Закон больших чисел относится к теории вероятностей и говорит о том, что среднее арифметическое какой-либо большой выборки из фиксированного распределения близко к математическому ожиданию этого распределения.

Домашнее задание

Задача 1. Среднее количество вызовов, поступающих на коммутатор завода в течение часа, равно 300. Оценить вероятность того, что в течение следующего часа число вызовов на коммутатор: а) превысит 400; б) будет не более 500.

Решение: По условию M X = 300.

а) Воспользуемся формулой (неравенством Маркова) (1).

Тогда вероятность того, что число вызовов превысит 400, будет не более 0,75. Проверить.

б) воспользуемся неравенством Маркова в альтернативном виде: (2)

Тогда вероятность того, что число вызовов не более 500, будет не менее 0,4. Проверить.

Задача 2. Генератор обеспечивает выходное напряжение, которое может отклоняться от

номинального на значение, не превышающее 1 В, с вероятностью 0,95. Какие значения

дисперсии выходного напряжения можно ожидать?

Решение. Пусть X - величина выходного напряжения. Применим неравенство Чебышева (4).

Ответ: дисперсия не менее 0,05 В 2 .

Задача 3. Дана последовательность независимых случайных величин X1,X2,...,Xn, Случайная величина Xk может принимать значения: −nα,0,nα (α>0) с вероятностями, соответственно равными: 1/2n²,1−1/n², 1/2n².Применим ли к этой последовательности закон больших чисел?

Решение. Для того чтобы к последовательности случайных величин была применима

теорема Чебышева, достаточно, чтобы эти величины были попарно независимы, имели

конечные математические ожидания и равномерно ограниченные дисперсии.

Поскольку случайные величины независимы, следовательно, они попарно независимы, то есть первое требование выполняется.

Проверить, что выполняется требование конечности математического ожидания:

Исследовать дисперсии и доказать, что дисперсии ограничены сверху. Вывод?