Рисунок 2.3 – Силы в зацеплении червячной передачи

Рисунок 2.3 – Силы в зацеплении червячной передачи

Окружная составляющая F_t₂ (Н) нормальной силы F_n (Н) на начальном диаметре колеса d_w₂ (мм) равна осевой составляющей F_х₁(Н) нормальной силы F_n (Н) на начальном диаметре червяка d_w₁

F_t₂= F_х₁ =2×10³×Т₂/ d_w₂ . (2.9)

Окружная составляющая F_t₁ (Н) нормальной силы F_n (Н) на начальном диаметре червяка d_w₁ (мм) равна осевой составляющей F_х₂(Н) нормальной силы F_n (Н) на начальном диаметре колеса d_w₂

F_t₁= F_х₂ = F_t₂× tg(g±j¢), (2.10)

где g - угол подъема линии витков червяка; j¢ - угол трения.

Угол трения j¢вычисляют на основании зависимости

tg j¢= f /cos a_n¢= f ¢, (2.11)

где a_n¢ - угол в нормальном сечении (tg a_n¢= tg a_х×соs g); f и f ¢ - коэффициенты трения.

Нормальная сила в зацеплении F_n (Н)

F_n = F_t₂ cos j¢/cos a_n¢×cos (g±j¢). (2.12)

Радиальная составляющая F_r₁ (Н) нормальной силы F_n (Н) на начальном диаметре червяка d_w₁ (мм) равна радиальной составляющей F_r₂(Н) нормальной силы F_n (Н) на начальном диаметре колеса d_w_{2 .}

F_r₁= F_r₂= F_n×sin a_n¢ = F_t₂×tg a_n¢ / соs g. (2.13)

Для установления величины усилий в зацеплении планетарных передач всех типов рассматривают равновесие каждого звена под действием внешних нагрузок

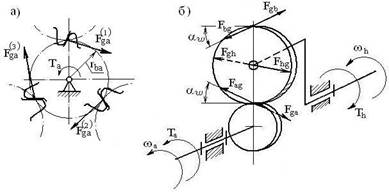
Рисунок 2.4 – Силы в планетарной зубчатой передаче:

a) – распределение усилий между колесами; б) – силы в зацеплении

( F⁽¹⁾_g_а, F⁽²⁾_g_а, F⁽³⁾_g_а–силы, действующие между сателлитом и центральным колесом а; F_gb – сила, действующая между сателлитом и центральным колесом b; Т_а, Т_h – моменты вращающие на центральном колесе и водиле соответственно; w_a, w_h – угловые скорости на центральном колесе и водиле соответственно; F_hg – сила, действующая между водилом и сателлитом)

Силы в зацеплении сателлита с центральным колесом рассчитывают с учетом коэффициента неравномерности нагрузки К_Н по наиболее нагруженному сателлиту. В расчетах опор сателлитов необходимо учитывать центробежную силу. Радиальные составляющие сил, действующих в передаче, которая имеет несколько сателлитов, не учитывают, т.к. они уравновешивают друг друга.

В трехсателлитной передаче (рисунок 2.4) вращающий момент Т_а на центральном колесе ауравновешивается силами F⁽¹⁾_g_а, F⁽²⁾_g_а, F⁽³⁾_g_а

Т_а=r_ba×( F⁽¹⁾_g_а+F⁽²⁾_g_а+F⁽³⁾_g_а , (2.14)

где r_ba – радиус основной окружности центрального колеса.

В идеальной передаче силы равны и нормальная сила от сателлита F_g_а

F_g_а = Т_а/( r_ba×n_w). (2.15)

В случае передачи с числом сателлитов n_w>3 неравномерность рас-пределения нагрузки исключить не удается и это учитывается умножением силы F_g_а на коэффициент неравномерного распределения нагрузки К_Н. Участие сателлита одновременно в двух зацеплениях приводит к тому, что одновенцовый сателлит не передает вращающий момент и находится в равновесии под действием сил F_а_g, F_bg и F_hg со стороны колес a, bи водила h соответственно.

Учитывая, что углы зацепления a_w одинаковы, из уравнения равновесия

F_hg =2× F_а_g×К_Н×cos a_w. (2.16)

Сила F_hg необходима при расчете подшипника сателлита и оси водила. Нормальную силу F_n , приходящуюся на единицу длины контактной линии l, называют удельной нагрузкой

w_m=F_n/l. (2.17)

Рабочая нагрузка равна произведению удельной нагрузки на корректирующие коэффициенты (коэффициенты режима нагружения, неравномерности распределения нагрузки, динамического влияния и т.п.), которые устанавливаются в каждом конкретном случае с учетом принятых критериев работоспособности. В расчетах оценивают нагрузку, которая вызывает наибольшее опасное напряжение для данного вида повреждения.

Расчет нагрузок, изменяющихся во времени, может быть произведен по одному из нижеприведенных методов (ГОСТ 21354 – 87).

Метод эквивалентных циклов ориентирован на приведение переменной нагрузки к величинам, вызывающим наибольшее повреждение элементов передачи. При расчете на контактную выносливость за исходную нагрузку Т_1Н принимают наибольшую из подводимых к передаче, для которой число циклов перемены напряжений не менее 0,03×N_Нlim1; соответствующее этой нагрузке эквивалентное число циклов напряжений N_НЕ1

N_НЕ1 =m_Н× N_Нlim1, (2.18)

где N_Нlim1 – базовое число циклов нагружений; m_Н – коэффициент, учитывающий характер циклограммы.

Для ступенчатой циклограммы m_Нравен

m_Н =å( Т_1i / Т_1Н)³(N_ci/N_Нlim1) . (2.92)

При плавном характере циклограммы величина m_Н

m_Н = 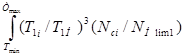. (2.19)

При расчете на выносливость при изгибе за исходную расчетную нагрузку Т_1F (или Т_2F) принимают наибольшую длительно действующую с числом циклов перемены напряжений более 5×10⁴; соответствующее этой нагрузке эквивалентное число циклов напряжений N_FЕ

N_F_Е =m_F× N_Flim , (2.20)

где m_F – коэффициент, учитывающий характер циклограммы

m_F =å( Т₁_i /Т₁_F)^qF×(N_ci/ N_Н_lim₁), (2.31)

где q_F –показатель степени кривой выносливости при циклическом изгибе.

Метод эквивалентных моментов предусматривает, что эквивалентный момент учитывает значение и длительность всех уровней нагрузки:

- при расчете на контактную выносливость за исходную расчетную нагрузку Т_1Н (или Т_2Н ) принимают эквивалентный момент

Т_НЕ =Т_max[å(T_i/T_max)³×(N_ci /N_K)]^1/3 ; (2.22)

- при расчете на выносливость при изгибе за исходную расчетную нагрузку Т_1F (или Т_2F) принимают эквивалентный момент

Т_FЕ =Т_max[å(T_i/T_max)³×(N_ci / N_K)]^1/^q^F , (2.23)

Метод эквивалентных напряженийоснован на определении расчетного напряжения для каждой ступени циклограммы:

- при расчете на контактную выносливость эквивалентное напряжение s_НЕ

s_НЕ=К_НЕ×s_Н1, (2.24)

где s_Н1 –расчетное напряжение соответствующее первой ступени циклограммы; К_НЕ - коэффициент эквивалентности, который равен:

К_НЕ =[å(s_Нi/s_Н1)⁶×(N_ci / N_Н_å)]^1/6 при s_Нi>s_Нlim; (2.25)

К_НЕ =[å(s_Нi/s_Н1)²⁰×(N_ci / N_Н_å)]^1/20 при s_Нi£s_Нlim, (2.26)

где N_Н_å – суммарное число циклов всех ступеней циклограммы; s_Нi – расчетное напряжение, соответствующее i -й ступени циклограммы (s_Нi³0,75×s_Нlim ); N_ci – соответствующее этой ступени число циклов перемены напряжений (N_ci ³0,03 ×N_Нlim);

-при расчете на выносливость при изгибе эквивалентное напряжение s_FЕ определяют по формуле

s_FЕ=К_FЕ×s_F1, (2.27)

где s_F1– расчетное напряжение соответствующее первой ступени циклограммы; К_FЕ - коэффициент эквивалентности

К_FЕ =[å(s_Fi/s_F1)^q^F×(N_ci/N_F_å)]^1/^q^F , (2.28)

где N_F_å -суммарное число циклов всех ступеней циклограммы, принятых в расчете на изгиб-

ную выносливость; s_F_i - расчетное напряжение, соответствующее i -й ступени циклограм-

мы; N_ci - соответствующее этой ступени число циклов перемены напряжений; q_F – показатель кривой выносливости.

Контактное напряжение s_Н (МПа) в полюсе зацепления равно

s_Н =s_Н0×(К_Н)^1/2, (2.29)

где s_Н0– контактное напряжение без учета дополнительных нагрузок, МПа; К_Н – коэффициент неравномерности распределения нагрузки.

Коэффициент нагрузки К_Н

К_Н = К_А× К_Н_v × К_Н_b × К_Н_a, (2.30)

где К_А – коэффициент, учитывающий внешнюю динамическую нагрузку;

К_Н_v – коэффициент, учитывающий внутреннюю динамическую нагрузку;

К_Н_b – коэффициент, учитывающий неравномерность распределения нагрузки по длине контактных линий; К_Н_a – коэффициент, учитывающий распределение нагрузки между зубьями.

Величину контактного напряжения s_Н0 (МПа) в зависимости от: окружного усилия F_t (Н) на делительном цилиндре в торцовом сечении, делительного диаметра d₁(мм) ведущего элемента, рабочей ширины b_w (мм) венца контактирующих элементов и передаточного числа устанавливают по следующей зависимости

s_Н₀=Z_E×Z_H×Z_e×Z_b×[F_t×(u+1)/(b_w×d₁×u)]^1/2, (2.31)

где Z_E – коэффициент, учитывающий механические свойства материалов сопряженных зубчатых колес

Z_Е ={E_пр/[p×(1– m²)]}^1/2 ; (2.32)

Z_H – коэффициент, учитывающий форму сопряженных поверхностей зубьев в полюсе зацепления (влияние радиусов кривизны боковых поверхностей и переход от окружной силы на делительном цилиндре на нормальную на начальном цилиндре)

Z _Н =(1/cos a_t)×(2×cos b_b /sina_w)^1/2 ; (2.33)

Z_e – коэффициент, учитывающий суммарную длину контактных линий

Z _e=(1/e_a)^1/2; (2.34)

Z_b –коэффициент, учитывающий наклон зуба.

Допускаемое контактное напряжение s_НР (МПа) не вызывающее опасной контактной усталости материала при минимальном запасе прочности S_Hmin,

s_НР =s_Н_lim× Z_L×Z_R×Z_v×Z_w×Z_X/S_Hmin, (2.35)

где s_Н_lim – предел контактной выносливости поверхностей зубьев, соответствующий эквивалентному числу циклов напряжений, МПа; Z_L – коэффициент, учитывающий влияние вязкости смазочного материала; Z_R – коэффициент, учитывающий влияние шероховатости сопряженных поверхностей зубьев; Z_v– коэффициент, учитывающий влияние окружной скорости; Z_w – коэффициент, учитывающий влияние перепада твердостей материалов сопряженных поверхностей зубьев ( 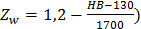, ; Z_X – коэффициент, учитывающий размер зубчатого колеса.

Предел контактной выносливости s_Нlim (МПа) равен

s_Нlim=s_Нlimb ×Z_N, (2.36)

где s_Нlimb – предел контактной выносливости, соответствующий базовому числу циклов напряжений, МПа; Z_N – коэффициент долговечности. Коэффициент долговечности Z_N

Z_N =(N_Hlim/N_К)^1/^q, (2.37)

где N_Hlim – базовое число циклов перемены напряжений, соответствующее пределу выносливости при контактных напряжениях; N_К –суммарное число циклов напряжений за весь срок службы (при использовании метода эквивалентных циклов вместо N_К подставляют N_НЕ); q – показатель степени кривой выносливости при контактных напряжениях.

Допускаемое предельное контактное напряжение (s_НР_max), не вызывающее остаточной деформации или хрупкого разрушения поверхностного слоя

s_Н_Pmax =s_Н_S_t/S_Н_S_t_min, (2.38)

где s_Н_S_t – предельное контактное напряжение при действии максимальной (пиковой) нагрузки; S_Н_S_t_min – минимальный коэффициент запаса прочности по максимальным контактным нагрузкам.

Нагрузочная способность поверхности зубьев обеспечивается при выполнении любого из критериев:

- критерия напряжений

s_Н £s_Н_P, (2.39)

s_Н_max £s_НР_max; (2.40)

- критерия безопасности

S_Н³ S_Н_min, (2.41)

S_Н_S_t³ S_Н_S_t_min; (2.42)

- критерия ресурса

N_L³ N_K, (2.43)

s_Н_max £s_НР_max; (2.44)

- критерия вероятности безотказной работы

Р_Н(N_L³ N_K)³Р_Н_min, (2.45)

Р_Н_S_t(s_Н_S_t³s_Н_max)³ Р_Н_S_t_min. (2.46)

В этих формулах S_Н – расчетный коэффициент запаса прочности для предотвращения опасной контактной усталости; S_Н_S_t – расчетный коэффициент запаса прочности для предотвращения опасных разрушений поверхностного слоя при максимальной нагрузке; s_Н_max – максимальное контактное напряжение за весь срок службы; N_L – число циклов напряжений в соответствии с расчетным сроком службы; N_K– число циклов напряжений в соответствии с заданным сроком службы; Р_Н– вероятность безотказной работы в течении заданного срока службы; Р_Н_min – минимальное регламентированное значение Р_Н; Р_Н_S_t – вероятность безотказной работы при расчете по максимальным контактным нагрузкам;

Р_Н_S_t_min – минимальное регламентированное значение Р_Н_S_t.

Напряжение изгиба s_F (МПа) в опасном сечении на переходной поверхности контактирующих элементов в зависимости от окружной силы F_t (Н) на делительном диаметре (в торцовом сечении), ширины b_w (мм) венца зубчатого колеса и нормального модуля m_n устанавливают по

следующей формуле

s_F = F_t×K _F×Y_FS×Y_b×Y_e/(b_w×m_n), (2.47)

где Y_FS – коэффициент, учитывающий форму зуба и концентрацию напряжений (зависит от количества зубьев на колесе и величины смещения инструмента при нарезании зуба); Y _b – коэффициент, учитывающий влияние угла наклона зуба; Y_e – коэффициент, учитывающий влияния перекрытия зубьев; K _F – коэффициент нагрузки.

Коэффициент нагрузки

K _F = К_А× К_F_v × К_F_b × К_F_a, (2.48)

где К_А – коэффициент, учитывающий внешнюю динамическую нагрузку; К_F_v – коэффициент, учитывающий внутреннюю динамическую нагрузку; К_F_b – коэффициент, учитывающий неравномерность распределения нагрузки по длине контактных линий; К_F_a – коэффициент, учитывающий распределение нагрузки между зубьями.

Допускаемое напряжение изгиба s_F_Р(МПа) на переходной поверхности, не вызывающее усталостного разрушения материала при минимальном коэффициенте запаса прочности S_Fmin

s_F_Р =s_Flimb×Y_N×Y_R×Y_X×Y_d/S_Fmin, (2.49)

где s_Flimb – предел выносливости зубьев при изгибе, МПа; Y_N – коэффициент долговечности; Y_R – коэффициент, учитывающий влияние шероховатости переходной поверхности; Y_X – коэффициент, учитывающий размер колеса; Y_d –коэффициент, учитывающий чувствительность материала к концентрации напряжений и градиенту напряжений (опорный коэффициент).

Предел выносливости зубьев при изгибе s_Flimb

s_Flimb =s⁰_Flimb×К, (2.50)

где s⁰_Flimb – предел выносливости зубьев при изгибе, соответствующий базовому числу циклов напряжений, МПа; К – коэффициент, учитывающий технологию изготовления, способ получения заготовки, влияние шлифования, деформационного упрочнения и реверсивность (при одностороннем приложении нагрузки К»1).

Коэффициент долговечности Y_N

Y_N =(N_Flim/N_К)^1/^q, (2.51)

где N_Fhlim – базовое число циклов перемены напряжений, соответствующее пределу выносливости материала при изгибе; N_К – суммарное число циклов напряжений за весь срок службы (при использовании метода эквивалентных циклов вместо N_К подставляют N_F_Е).

Фактические значения контактных напряжений и напряжений изгиба не должны превышать допускаемых величин, что является основанием для установления геометрических параметров передачи.

Проектный расчет закрытых передач ведут по допускаемым контактным напряжениям с последующей проверкой по напряжениям изгиба. Расчет открытых передач производят по допускаемым напряжениям с последующей проверкой по контактным напряжениям. Допускаемое напряжение изгиба в опасном сечении (s_F_р_max), не вызывающее остаточной деформации, хрупкого излома или первичных трещин равно

s_Fpmax =(s_FS_t/S_Fs_t_min)×(Y_d_S_t/Y_d_S_t_T), (2.52)

где s_FS_t – предельное напряжение изгиба при действии максимальной

нагрузке; S_Fs_t_min – минимальный коэффициент запаса прочности по максимальным нагрузкам; Y_d_S_t – опорный коэффициент при максимальной нагрузке; Y_d_S_t_T – опорный коэффициент испытываемого зубчатого колеса при максимальной нагрузке.

Нагрузочная способность зуба при изгибе обеспечивается при выполнении любого из критериев:

- критерия напряжений

s_F £s_FP, (2.53)

s_Fmax £s_F_р_max; (2.54)

- критерия безопасности

S_F³ S_Fmin, (2.55)

S_FS_t³ S_FS_t_min; (2.56)

- критерия ресурса

N_L³ N_K, (2.57)

s_Fmax £s_F_Р_max; (2.58)

- критерия вероятности безотказной работы

Р_F (N_L³ N_K)³Р_Fmin, (2.59)

Р_FS_t(s_FS_t³s_Fmax) ³ Р_FS_t_min. (2.60)

В этих формулах S_F–расчетный коэффициент запаса прочности для предотвращения усталостного разрушения материала; S_FS_t – расчетный коэффициент запаса прочности для предотвращения опасных повреждений при максимальной нагрузке; s_Fmax – максимальное местное напряжение от изгиба в опасном сечении за весь срок службы; N_L – число циклов напряжений в соответствии с расчетным сроком службы; N_K – число циклов напряжений в соответствии с заданным сроком службы; Р_F – вероятность отсутствия повреждений в течении заданного срока службы; F_Н_min – минимальное регламентированное значение Р_F; Р_FS_t – вероятность отсутствия хрупкого излома или остаточной деформации при максимальной нагрузке; Р_FS_t_min –минимальное регламентированное значение Р_FS_t

⇐ Предыдущая 12