Лекция: Формулы приведения. Ссылка на видео: https://cknow.ru/knowbase/510-125-formuly-privedeniya.html

	государственное бюджетное профессиональное образовательное учреждение «Пермский торгово-технологический колледж»
	ЗАДАНИЯ ДЛЯ ВЫПОЛНЕНИЯ В ДИСТАНЦИОННОЙ ФОРМЕ
Ф.И.О. педагога	Стринкевич Лилия Ильфатовна
Данные для обратной связи	https://vk.com/club199606690
Наименование дисциплины	Математика
Тема занятия	Формулы приведения
Срок выполнения	18.11.2020
Алгоритм выполнения дистанционного задания	1. Законспектировать тему и выполнить задание в рабочей тетради (ответы без решения не принимаются). 2. Отправляем сообщение с фотографиями выполненной работы в группу: https://vk.com/club199606690

Лекция: Формулы приведения

Ссылка на видео: https://cknow.ru/knowbase/510-125-formuly-privedeniya.html

Из прошлых тем нам известно, что тригонометрические функции являются периодичными функциями, именно поэтому при рассмотрении любых углов, их можно свести ко всем углам, находящимся на единичной окружности. Более того, любой угол можно свести к острому углу. Чтобы это сделать, необходимо знать формулы приведения.

Итак, давайте возьмем произвольный угол, который находится, например, в пределе от π до 3π/2. Данный угол можно записать следующим образом: (π + α). В данном случае α - острый угол. А теперь давайте определим, в какой четверти мы оказались.

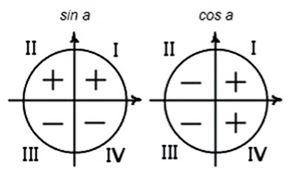
От π до 3π/2 - это третья четверть. В данной четверти и синус, и косинус имеет отрицательное значение. Для нахождения косинуса или синуса данного угла имеем право: cos(π + α) = -cos α. Полученное выражение называется одной из формул приведения. Данные уравнения можно получить для любой функции, в зависимости от знака данной четверти.

Формулы приведения

Чтобы переходить от больших углов к острым совершенно не обязательно знать огромное множество формул приведений, достаточно понимать, как они были получены.

Для того, чтобы лучше понять, давайте рассмотри несколько примеров:

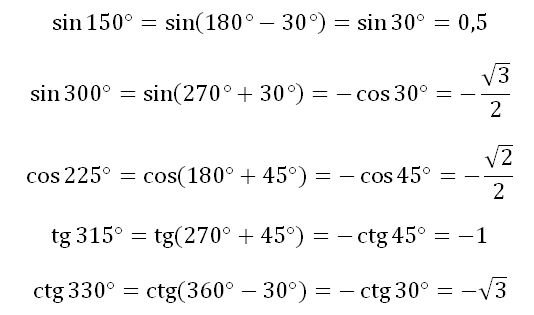
Итак, рассмотрим первый пример, описанный выше. Чтобы воспользоваться формулами приведения и прийти к острым углам, следует выделить π или 2 π. Чтобы не изменить величину аргумента, а также выделить π, необходимо от 180 отнять 30. Это означает, что в единичной окружности необходимо переместиться в точку π. Далее мы видим знак минус - это означает, что для того, чтобы отложить данный угол, следует двигаться по часовой стрелке, то есть от π отложить угол 30 градусов, или π/6. Мы оказались во второй четверти. Как мы уже знаем, величины углов во второй четверти являются положительными, так как здесь ордината принимает положительные значения. А это значит, что мы можем отбросить π и найти синус 30 градусов.

Аналогичные вычисления можно сделать и с другими примерами.

12 Следующая ⇒