Хелпикс

Главная

Контакты

Случайная статья



Одинаковые спектры разных сигналов



Одинаковые спектры разных сигналов

 

Сейчас мы увидим, что импульсы разной длительности имеют почти одинаковые спектры и только постоянная составляющая у них, конечно, разная. На рис. 1 изображены периодические последовательности импульсов, имеющих разную длительность.

У верхних τ2 = 5/6 T, а у нижних τ1 = 1/6 T.

 

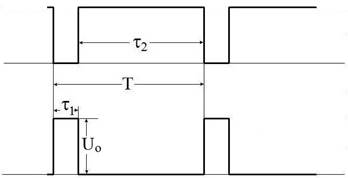
Рис. 1.

 

Если с умом выбрать начало отсчёта времени, то для нижних, коротких импульсов можно написать гармоники ряда Фурье в виде:

 

 

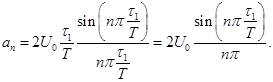                                                           (1)

Для верхних ряд будет такой:

 

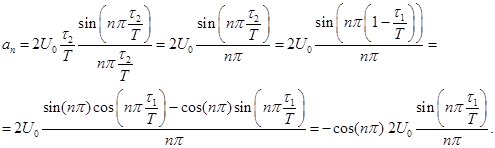
       (2)

 

Модули спектральных составляющих этих двух спектров совпадают. А постоянная составляющая, т.е. член a0/2  у верхних импульсов в пять раз больше.

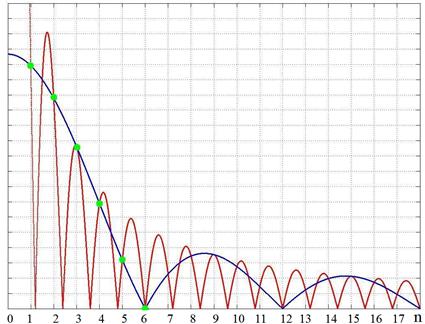Интересно посмотреть, как реализовано совпадение двух этих спектров. Для этого на рис. 2 построены их огибающие sin x/x. Они пересекаются как раз на частотах гармоник.

 

Первые шесть пересечений отмечены точками.

 

Рис. 2.

 

 
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.