У меня нет по этому вопросу лекции, не знаю что писать!!!!

16-20 ответы.

16. вопрос.

Регрессия - одно из основных понятий в теории вероятности и математической статистике, выражающее зависимость среднего значения случайной величины от значений другой случайной величины или нескольких случайных величин. Теоретическая линия регрессии - это та линия, вокруг которой группируются точки корреляционного поля и которая указывает основное направление, основную тенденцию связи.
Теоретическая линия регрессии должна отображать изменение средних величин результативного признака «y» по мере изменения величин факторного признака «x» при условии полного взаимопогашения всех прочих – случайных по отношению к фактору «x» - причин. Следовательно, эта линия должна быть проведена так, чтобы сумма отклонений точек поля корреляции от соответствующих точек теоретической линии регрессии равнялась нулю, а сумма квадратов этих отклонений была ба минимальной величиной.
y=f(x) - уравнение регрессии - это формула статистической связи между переменными.
Прямая линия на плоскости (в пространстве двух измерений) задается уравнением y=a+b*х. Более подробно: переменная y может быть выражена через константу (a) и угловой коэффициент (b), умноженный на переменную x. Константу иногда называют также свободным членом, а угловой коэффициент - регрессионным или B-коэффициентом.
Важным этапом регрессионного анализа является определение типа функции, с помощью которой характеризуется зависимость между признаками Наиболее часто для характеристики связей экономических показателей используют следующие типы функций:
1. Линейная: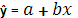

17.вопрос метод наименьших квадрадов(МНК)-классический подход к оцениван. параметров линейной регрессии. МНК позволяет получить такие оценки параметров а и в, при которых сумма квадратов отклонений фактически знач. результативного признака y от расчетных(теоретических) у^ минимальны т.е 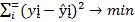,иными словами ξi=yi-ŷ Для того, чтобы найти минимум ф-ции, надо вычитать частные производные по каждому из парам.(а)и(в) и прировнять их к нулю S=Σ 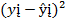=Σ(y-а-bх)², у=а+вх. Метод наименьших квадратов— один из базовых методов регрессионного анализа для оценки неизвестных параметров регрессионных моделей по выборочным данным. Метод основан на минимизации суммы квадратов остатков регрессии.

18 вопрос

Дисперсия, как видно, представляет собой сумму к.в а д р а т о в возможных отклонений случайной величины от ее среднего значения, взятых с «весовыми» коэффициентами, равными вероятностям соответствующих отклонений. Говоря иначе, она представляет собой математическое ожидание квадратов отклонений случайной величины от ее среднего значения.

Математи́ческое ожида́ние — среднее значение случайной величины, распределение вероятностей случайной величины, рассматривается в теории вероятностей.

У меня нет по этому вопросу лекции, не знаю что писать!!!!

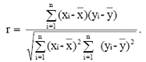19. вопрос Уравнение регрессии всегда дополняется показателями тесноты связи. При использовании линейной регрессии в качестве такого показателя выступает линейный показатель корреляции rху =b*

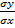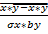, σ-среднеквадратное отклонение, cov-ковариация. приделы -1<rxy<1. Чем ближе коэф.кореляции, тем теснее связь между переменными и тем ближе она к линейной. Тесноту и направление парной линейной корреляционной связи измеряют с помощью линейного коэффициента корреляции (1.1.10), принимающего значения в пределах от –1 до +1. Квадрат коэффициента корреляции называют коэффициентом детерминации (r²). Коэффициент детерминации можно интерпретировать как долю общей дисперсии результативного признака (y), которая объясняется вариацией факторного признака (x). Значимость линейного коэффициента корреляции проверяется на основе t-критерия Стьюдента: проверяется нулевая гипотеза об отсутствии связи между факторным и результативным признаками (H₀: r = 0).

20 вопрос При проведении статист. исследования возникает необходимость фор-ки и эксперементальной проверки. Статистическая гипотеза- это предложение о случайной величине, проверяемой по выборке(результатам наблюдения). Будем обозначать высказанные предположения(гипотезу)буквой H. Процедура сопоставления высказанной гипотезы с имеющимися выборочными данными и количественная оценка степени достоверности полученного вывода называется - статист.проверкой гипотез. Существует множество разнообразных критериев. Однако, они строятся по общей логической системе: 1)выдвигается гипотеза. Ho - основной или нулевой; 2) задается величина уровня значимости α. Принятие статистич. Решения всегда сопровождается некоторой вероятностью. Как в одну так и в другую сторону. В небольшой доле случаев α, гипотеза Ho-может быть отвергнута, в то время как на самом деле является справедливой. В какой то доле случая β, мы можем принять гипотезу, в то время как на самом деле она ошибочна. 3) задается некоторая функция, которую называют критич. статистикой. 4)из соответ.таблиц распределения, наход.критическое значение для статистического критерия. 5)осуществ. Сравнение фактического значения с табличными значениями и делается вывод о достоверности провер.гипотез. В регрессионном анализе проверкам статистической значимости подвергаются: -сама регрессия; -коэфф. Регрессии; -корреляция.