Пример для матрицы А размером 5 х 5 и вектора Y размером 5.

Пример для матрицы А размером 5 х 5 и вектора Y размером 5.

Задание 5.

Метод наименьших квадратов

Данные о росте безработицы 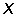, % и росте преступности 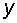, % приведены в таблице (рис. 1).

Рис. 1

1. Методом наименьших квадратов по табличным данным найти аппроксимирующие (приближаемые) функции, то есть регрессии: линейную, квадратичную, показательную, гиперболическую.

2. В каждом случае найти общую ошибку и среднюю ошибку аппроксимации. Указать функцию лучшей аппроксимации.

3. Построить линии регрессии на одной плоскости вместе с исходными данными.

Таблицу (рис. 1) можно считать функцией, заданной таблично.

Алгоритм решения задачи

1. Определим систему нормальных уравнений для нахождения оценок параметров линейной регрессии:

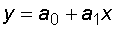1.1. В целях удобства расчетов представим таблицу исходных данных следующим образом (рис. 2), которую дополним еще двумя расчетными столбцами: и .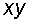

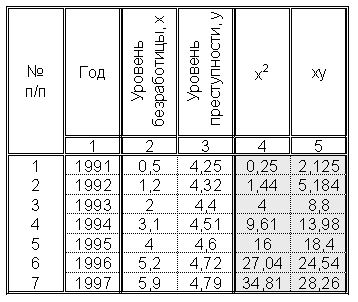
Рис. 2

1.2. В верхнюю ячейку столбца 4 введем формулу и автоматически заполним весь столбец (путем протягивания ячейки с формулой на область заполнения).

=СТЕПЕНЬ(«верхняя ячейка столбца x»;2)

Вызов функции: MS Excel – Вставка – Функция… – Математические

1.3. В верхнюю ячейку столбца 5 введем формулу и автоматически заполним весь столбец (путем протягивания ячейки с формулой на область заполнения).

=«верхняя ячейка столбца x»*«верхняя ячейка столбца y»

1.4. Просуммируем значения столбцов: 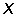, , 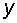, 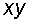с помощью функции СУММ, а результат суммирования запишем под столбцом с соответствующими данными (рис. 3).

Получаем систему нормальных уравнений для линейной регрессии:

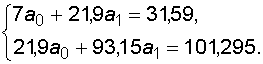
Рис. 3

Замечание. Данную систему нормальных уравнений можно решать и методом Крамера, и матричным методом. Однако мы будем использовать для ее решения надстройку MS Excel Поиск решения….

2. Решаем систему нормальных уравнений для линейной регрессии.

2.1. Составим исходную табличную модель для решения системы линейных алгебраических уравнений с помощью надстройки Поиск решения... (рис. 4).

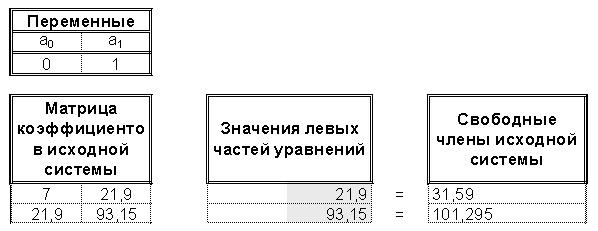
Рис. 4

2.2. В блок «Переменные» в первую строку записываем переменные системы алгебраических уравнений.

2.3. В блок «Переменные» во вторую строку записываем произвольные числовые значения (удобнее в качестве числовых значений поставить номера переменных), затем, после выполнения команды Поиск решения..., в этих ячейках получим исходные решения системы.

2.4. В блок «Матрица коэффициентов исходной системы» записываем соответствующую матрицу коэффициентов при переменных , .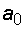

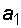2.5. В блок «Значения левых частей уравнений» в верхнюю ячейку вводим формулу:

=СУММПРОИЗВ(«фиксированный диапазон строки значений переменных 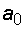, 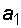»;«диапазон первой строки матрицы коэффициентов исходной системы»)

2.6. Автоматически заполняем весь столбец «Значения левых частей уравнений».

2.7. В блок «Свободные члены исходной системы» в столбец записываем значения правой части исходной системы.

2.8. Вызываем Поиск решения и заполняем форму:

Вызов Поиск решения...: MS Excel – Данные – Поиск решения…

Замечание. Если в меню Данные нет команды Поиск решения…, значит, надстройка не подключена. Подключение выполняется в окне Меню - Параметры Excel - Надстройки установкой флажка перед опцией Поиск решения.

Установить целевую ячейку – ничего не ставить;

Равной – максимальному значению;

Изменяя ячейки – диапазон строки значений переменных;

Ограничения – диапазон «Значения левых частей уравнений» = диапазон «Свободные члены исходной системы»;

2.8.1. Заполнить форму Результаты поиска решений:

поставить опцию Сохранить найденное решение;

нажать ОК.

Результат выполнения команды Поиск решения… будет следующий (рис. 5)

Рис. 5

2.9. Изменить формат ячеек с полученным решением (строка значений переменных) так, чтобы было три знака после запятой.

3. Записываем уравнение линейной регрессии.

Уравнение линейной регрессии:

Исходные данные распределения добавленной стоимости по отраслям экономики в ЕС в 2002 г. (выбрать любую из пар зависимого и независимого показателей).

⇐ Предыдущая 12